BIOSTAT 725 - Spring 2025 – Multiclass Classification

Review of last lecture

On Tuesday, we learned about classification using logistic regression.
Today, we will focus on multiclass classification: multinomial regression, ordinal regression.

Multiclass regression

Often times one encounters an outcome variable that is nominal and has more than two categories.
If there is no inherent rank or order to the variable, we can use multinomial regression. Examples include:
- gender (male, female, non-binary),
- blood type (A, B, AB, O).
If there is an order to the variable, we can use ordinal regression. Examples include:
- stages of cancer (stage I, II, III, IV),
- pain level (mild, moderate, severe).

Multinomial random variable

Assume an outcome $Y_{i} \in {1, \dots, K}$ for $i = 1, \dots, n$ .
The likelihood in multinomial regression can be written as the following categorical likelihood,

$f (Y | β) = \prod_{i = 1}^{n} \prod_{j = 1}^{K} P (Y_{i} = j)^{δ_{i j}},$

$δ_{i j} = 1 (Y_{i} = j)$ is the Kronecker delta.
Since $Y_{i}$ is discrete, we only need to specify $P (Y_{i} = j)$ for all $i$ and $j$ .

Log-linear regression

One way to motivate multinomial regression is through a log-linear specification:

$\log P (Y_{i} = j) = x_{i} β_{j} - \log Z .$

$β_{j}$ is a $j$ specific set of regression parameters.
$P (Y_{i} = j) = \exp {x_{i} β_{j}} / Z$ .
$Z$ is a normalizing constant that guarentees that $\sum_{j = 1}^{K} P (Y_{i} = j) = 1$ .

Finding the normalizing constant

We know that,

$\begin{aligned} 1 & = \sum_{j = 1}^{K} P (Y_{i} = j) = \frac{1}{Z} \sum_{j = 1}^{K} \exp {x_{i} β_{j}} \\ ⟹ Z = \sum_{j = 1}^{K} \exp {x_{i} β_{j}} \end{aligned}$

Multinomial probabilities

Thus, we have the following,

$P (Y_{i} = k) = \frac{\exp {x_{i} β_{k}}}{\sum_{j = 1}^{K} \exp {x_{i} β_{j}}} .$

This function is called the softmax function.
Unfortunately, this specification is not identifiable.

Identifiability issue

We can add a vector $c$ to all parameters and get the same result,

$\begin{aligned} \frac{\exp {x_{i} (β_{k} + c)}}{\sum_{j = 1}^{K} \exp {x_{i} (β_{j} + c)}} & = \frac{\exp {x_{i} β_{k}}}{\sum_{j = 1}^{K} \exp {x_{i} β_{j}}} . \end{aligned}$

A common solution is to set: $β_{K} = 0$ .

Updating the probabilities

Using the identifiability constraint of $β_{K} = 0$ , the probabilities become, $\begin{aligned} P (Y_{i} = k) & = \frac{\exp {x_{i} β_{k}}}{1 + \sum_{j = 1}^{K - 1} \exp {x_{i} β_{j}}}, k \in {1, \dots, K - 1}, \\ P (Y_{i} = K) & = \frac{1}{1 + \sum_{j = 1}^{K - 1} \exp {x_{i} β_{j}}} . \end{aligned}$
How to interpret the $β_{k}$ ?

Deriving the additive log ratio model

Using our specification of the probabilities, it can be seen that,

$\begin{aligned} P (Y_{i} = k) & = \frac{\exp {x_{i} β_{k}}}{1 + \sum_{j = 1}^{K - 1} \exp {x_{i} β_{j}}} \\ = [\frac{1}{1 + \sum_{j = 1}^{K - 1} \exp {x_{i} β_{j}}}] \exp {x_{i} β_{k}} \\ = P (Y_{i} = K) \exp {x_{i} β_{k}} . \end{aligned}$

$⟹ \log \frac{P (Y_{i} = k)}{P (Y_{i} = K)} = x_{i} β_{k}, k \in {1, \dots, K - 1}$

Additive log ratio model

If outcome $K$ is chosen as reference, the $K - 1$ regression equations are:

$\log \frac{P (Y_{i} = k)}{P (Y_{i} = K)} = x_{i} β_{k}, k \in {1, \dots, K - 1}$

This formulation is called additive log ratio.
$β_{j k}$ represent the log-odds of being in category $k$ relative to the baseline category $K$ with a one-unit change in $X_{i j}$ .
- $\exp (β_{j k})$ is an odds ratio.

Getting back to the likelihood

The log-likelihood can be written as,

$\log f (Y | β) = \sum_{i = 1}^{n} \sum_{j = 1}^{K} δ_{i j} \log P (Y_{i} = j) .$

The $P (Y_{i} = j)$ are given by the additive log ratio model.
As Bayesians, we only need to specify priors for $β_{k}, k \in {1, \dots, K - 1}$ .

Multinomial regression in Stan

Hard coding the likelihood.

// additive_log_ratio.stan
functions {
  matrix compute_alr_probs(int n, int K, int p, matrix X, matrix beta) {
    matrix[n, K] probs;
    matrix[n, K - 1] expXbeta = exp(X * beta);
    for (i in 1:n) {
      real sum_i = sum(expXbeta[i, ]);
      for (j in 1:K) {
        if (j < K) {
          probs[i, j] = expXbeta[i, j] / (1 + sum_i);
        }
        if (j == K) probs[i, j] = 1 - sum(probs[i, 1:(K - 1)]);
      }
    }
    return probs
  }
}
data {
  int<lower = 1> K;
  int<lower = 1> n;
  int<lower = 1> p;
  array[n] int<lower = 1, upper = K> Y;
  matrix[n, p] X;
  matrix[n, K] delta;
}
parameters {
  matrix[p, K - 1] beta;
}
model {
  matrix[n, K] probs = compute_alr_probs(n, K, p, X, beta);
  for (i in 1:n) {
    for (j in 1:K) {
      target += delta[i, j] * log(probs[i, j]);
    }
  }
  target += normal_lpdf(to_vector(beta) | 0, 10);
}

Multinomial regression in Stan

Non-identifiable version.

// multi_logit_bad.stan
data {
  int<lower = 1> K;
  int<lower = 1> n;
  int<lower = 1> p;
  array[n] int<lower = 1, upper = K> Y;
  matrix[n, p] X;
}
parameters {
  matrix[p, K] beta;
}
model {
  matrix[n, K] Xbeta = X * beta;
  for (i in 1:n) {
    target += categorical_logit_lpmf(Y[i] | Xbeta[i]')
  }
  target += normal_lpdf(to_vector(beta) | 0, 10);
}

categorical_logit

Multinomial regression in Stan

Zero identifiability constraint.

// multi_logit.stan
data {
  int<lower = 1> K;
  int<lower = 1> n;
  int<lower = 1> p;
  array[n] int<lower = 1, upper = K> Y;
  matrix[n, p] X;
}
transformed data {
  vector[p] zeros = rep_vector(0, p);
}
parameters {
  matrix[p, K - 1] beta_raw;
}
transformed parameters {
  matrix[p, K] beta = append_col(beta_raw, zeros);
}
model {
  matrix[n, K] Xbeta = X * beta;
  for (i in 1:n) {
    target += categorical_logit_lpmf(Y[i] | Xbeta[i]')
  }
  target += normal_lpdf(to_vector(beta) | 0, 10);
}
generated quantities {
  matrix[p, K - 1] ors = exp(beta_raw);
  vector[n] Y_pred;
  vector[n] log_lik;
  for (i in 1:n) {
    Y_pred[i] = categorical_logit_rng(Xbeta[i]');
    log_lik[i] = categorical_logit_lpmf(Y[i] | Xbeta[i]');
  }
}

Ordinal regression

Let $Y_{i} \in {1, \dots, K}$ be an ordinal outcome with $K$ categories.

The likelihood in ordinal regression is identical to the one from multinomial regression,

$f (Y | β) = \prod_{i = 1}^{n} \prod_{j = 1}^{K} P (Y_{i} = j)^{δ_{i j}} .$

We need to add additional constraints that guarantee ordinality.

Proportional odds assumption

$P (Y_{i} \leq k)$ is the cumulative probability of $Y_{i}$ less than or equal to a specific category $k = 1, \dots, K - 1$ .
The odds of being less than or equal to a particular category can be defined as, $\frac{P (Y \leq k)}{P (Y > k)} for k = 1, \dots, K - 1.$
Not defined for $k = K$ , since division by zero is not defined.

Proportional odds regression

The log odds can then be modeled as follows, $\log \frac{P (Y_{i} \leq k)}{P (Y_{i} > k)} = logit P (Y_{i} \leq k) = α_{k} - x_{i} β$

Why $- β$ ?
$β$ is a common regression parameter. For a one-unit increase in $x_{i j}$ , $β_{j}$ is the change in log odds of moving to a more severe level of the outcome $Y_{i}$ .
$α_{k}$ for $k = 1, \dots, K - 1$ are $k$ -specific intercepts that corresponds to the log odds of moving from level $k$ to $k + 1$ .

Understanding the probabilities

One can solve for $P (Y_{i} \leq k), k = 1, \dots, K - 1$ ),

$P (Y_{i} \leq k) = \frac{\exp {α_{k} - x_{i} β}}{1 + \exp {α_{k} - x_{i} β}} = expit (α_{k} - x_{i} β) .$

$P (Y_{i} \leq K) = 1$ .

The individual probabilities are then given by,

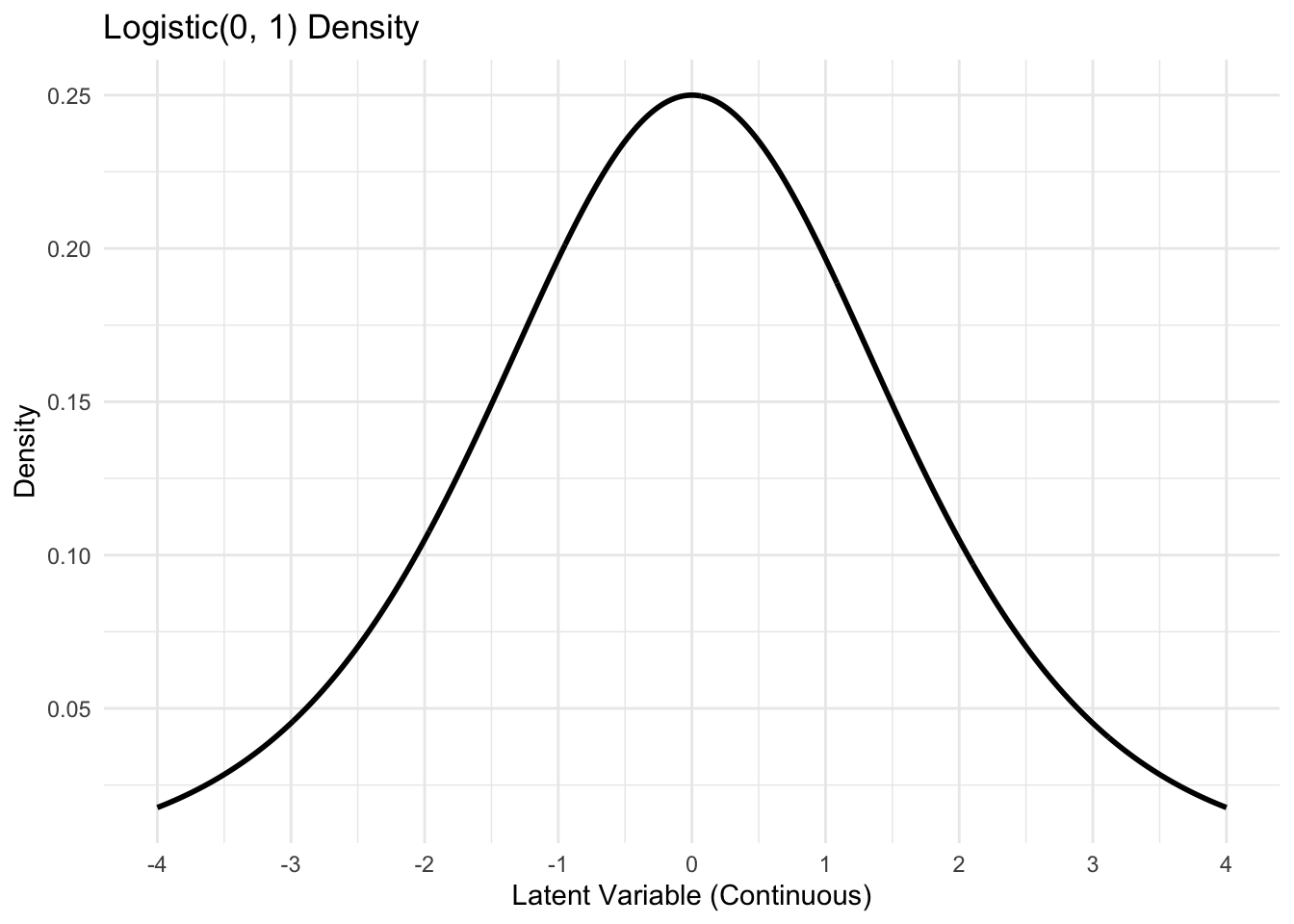
$\begin{aligned} P (Y_{i} = k) & = P (Y_{i} \leq k) - P (Y_{i} \leq k - 1) \\ = expit (α_{k} - x_{i} β) - expit (α_{k - 1} - x_{i} β) . \end{aligned}$

A latent variable representation

Define a latent variable,

$Y_{i}^{*} = x_{i} β + ϵ_{i}, ϵ_{i} \sim Logistic (0, 1) .$

$E [ϵ_{i}] = 0$ .
$V (ϵ_{i}) = π^{2} / 3$ .
CDF: $P (ϵ_{i} \leq x) = \frac{1}{1 + \exp {- x}} = \frac{\exp {x}}{1 + \exp {x}} = expit (x) .$

Visualizing the latent process

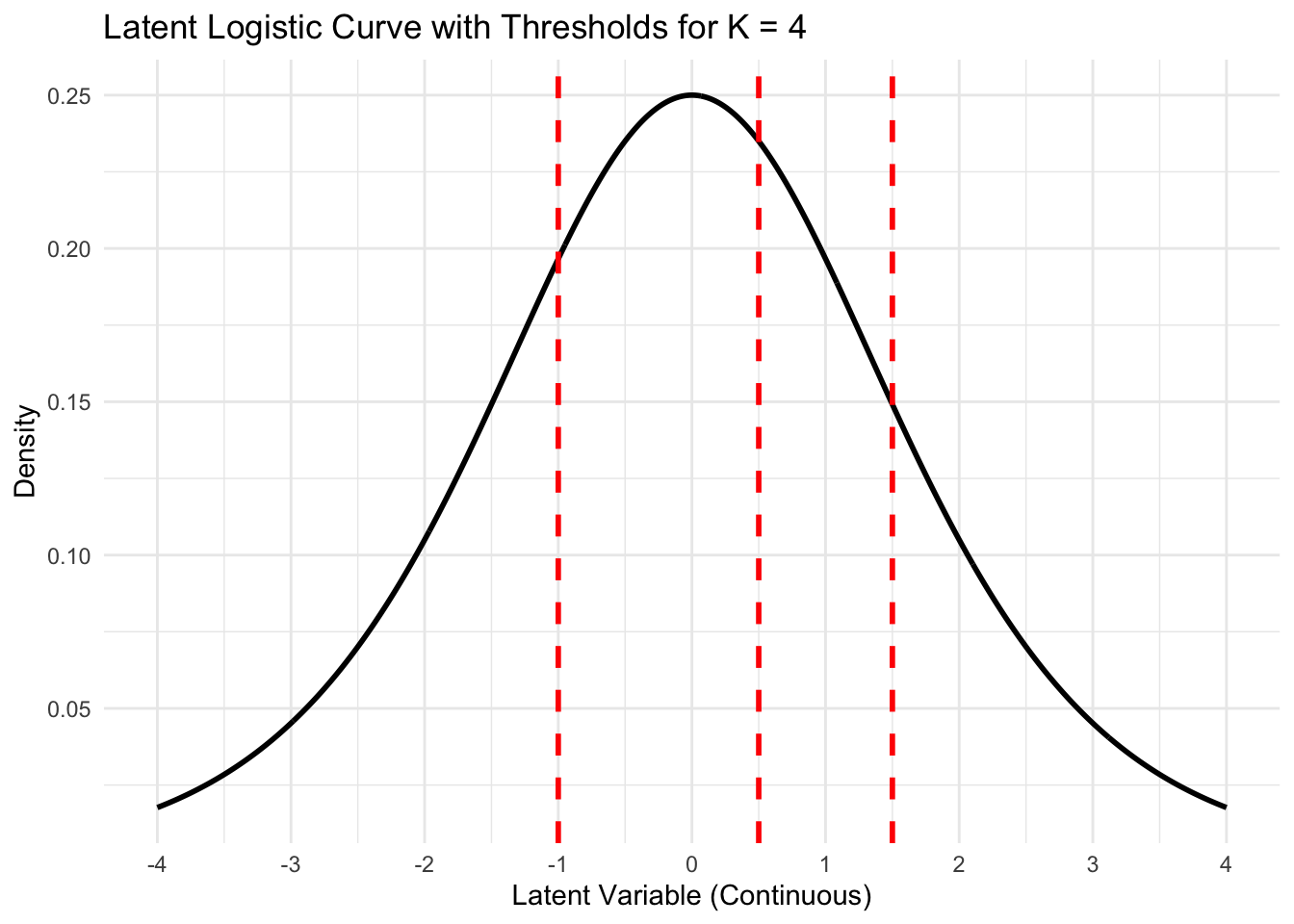
Adding thresholds ( $c_{k}$ )

Getting category probabilities

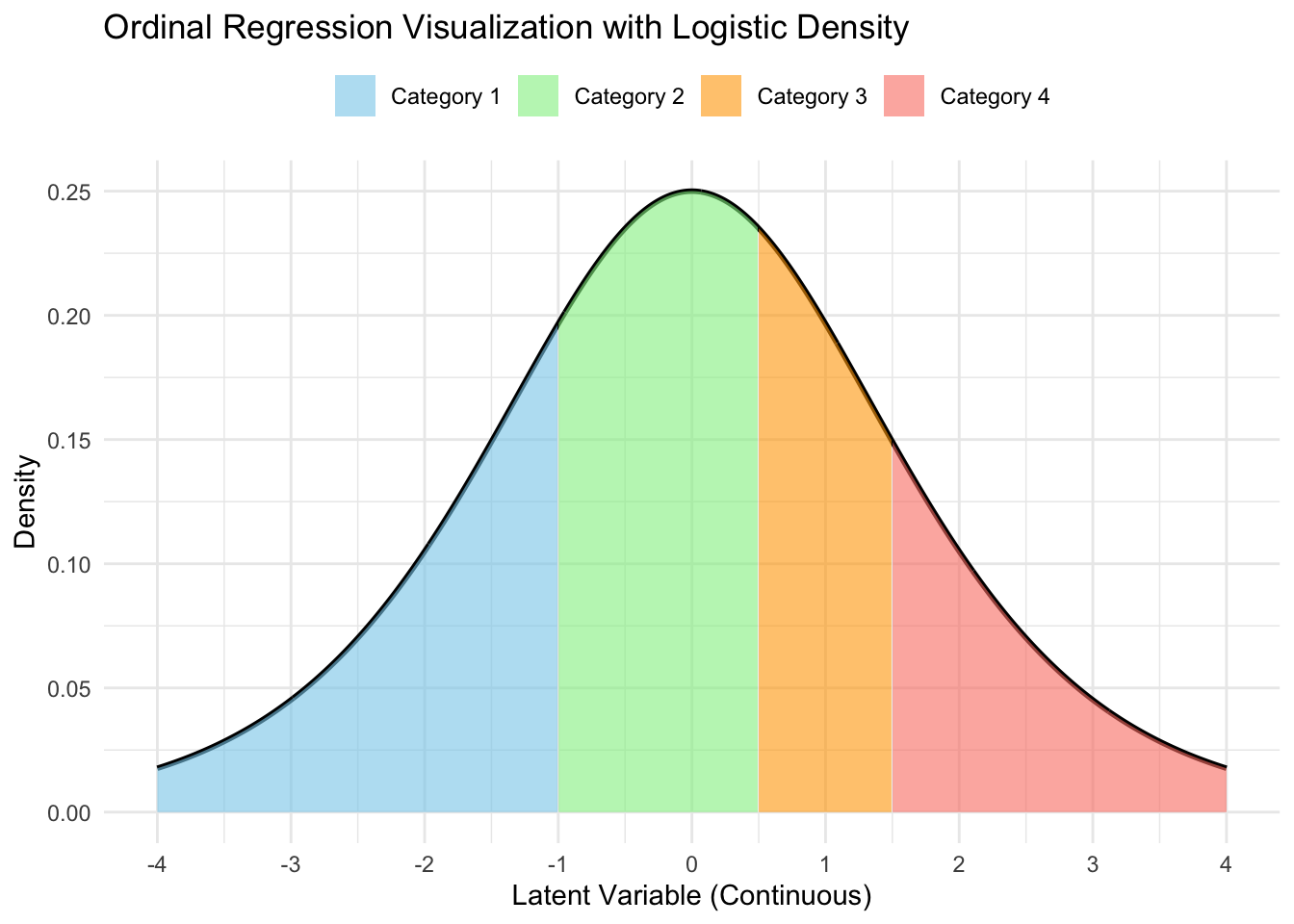
A latent variable representation

Define a set of $K - 1$ cut-points, $(c_{1}, \dots, c_{K - 1}) \in R^{K - 1}$ . We also define $c_{0} = - \infty, c_{K} = \infty$ .
Our ordinal random variable can be generated as,

$Y_{i} = {\begin{cases} 1 & c_{0} < Y_{i}^{*} \leq c_{1} \\ 2 & c_{1} < Y_{i}^{*} \leq c_{2} \\ ⋮ \\ K & c_{K - 1} < Y_{i}^{*} \leq c_{K} \end{cases}$

Equivalence of the two specifications

Probabilities under the latent specification: $\begin{aligned} P (Y_{i} = k) & = P (c_{k - 1} < Y_{i}^{*} \leq c_{k}) \\ = P (c_{k - 1} < x_{i} β + ϵ_{i} \leq c_{k}) \\ = P (x_{i} β + ϵ_{i} \leq c_{k}) - P (x_{i} β + ϵ_{i} < c_{k - 1}) \\ = P (ϵ_{i} \leq c_{k} - x_{i} β) - P (ϵ_{i} < c_{k - 1} - x_{i} β) \\ = expit (c_{k} - x_{i} β) - expit (c_{k - 1} - x_{i} β) . \end{aligned}$
Equivalency:
- $α_{k} = c_{k}, k = 1, \dots, K - 1$ , assuming that $α_{k} < α_{k + 1}$ .

Ordinal regression using Stan

// ordinal.stan
data {
  int<lower = 2> K;
  int<lower = 0> n;
  int<lower = 1> p;
  int<lower = 1, upper = K> Y[n];
  matrix[n, p] X;
}
parameters {
  vector[p] beta;
  ordered[K - 1] alpha;
}
model {
  target += ordered_logistic_glm_lpmf(Y | X, beta, alpha);
  target += normal_lpdf(beta | 0, 10);
  target += normal_lpdf(alpha | 0, 10);
}
generated quantities {
  vector[p] ors = exp(beta);
  vector[n] Y_pred;
  vector[n] log_lik;
  for (i in 1:n) {
    Y_pred[i] = ordered_logistic_rng(X[i, ] * beta, alpha);
    log_lik[i] = ordered_logistic_glm_lpmf(Y[i] | X[i, ], beta, alpha);
  }
}

ordered_logistic_glm_lpmf

Enforcing order in the cutoffs

In Stan, when you define a parameter as ordered[K-1] alpha;, the values of alpha are automatically constrained to be strictly increasing.
This transformation ensures that the alpha values follow the required order, i.e., alpha[1] < alpha[2] < ... < alpha[K-1].
Stan doesn’t sample alpha directly but instead works with an unconstrained parameter vector, which we will call gamma.

Enforcing order in the cutoffs

parameters {
  vector[K - 1] gamma;
}
transformed parameters {
  vector[K - 1] alpha;
  alpha[1] = gamma[1];
  for (j in 2:K) {
    alpha[j] = alpha[j - 1] + exp(gamma[j]);
  }
}

Here, gamma represents a vector of independent, unconstrained variables, and the transformation ensures that alpha is strictly increasing by construction.
Luckily we can use ordered, since Stan takes care of this (including the Jacobian) in the background.

Prepare for next class

Work on HW 03.
Complete reading to prepare for next Tuesday’s lecture
Tuesday’s lecture: Missing data