Bayesian Clustering
Apr 08, 2025
Learning Objectives
- We will introduce the basic mixture modeling framework as a mechanism for model-based clustering and describe computational and inferential challenges.
- Variations of the popular finite Gaussian mixture model (GMM) will be introduced to cluster patients according to ED length-of-stay.
- We present an implementation of mixture modeling in Stan and discuss challenges therein.
- Finally, various posterior summaries will be explored.
Finding subtypes
Revisiting data on patients admitted to the emergency department (ED) from the MIMIC-IV-ED demo.
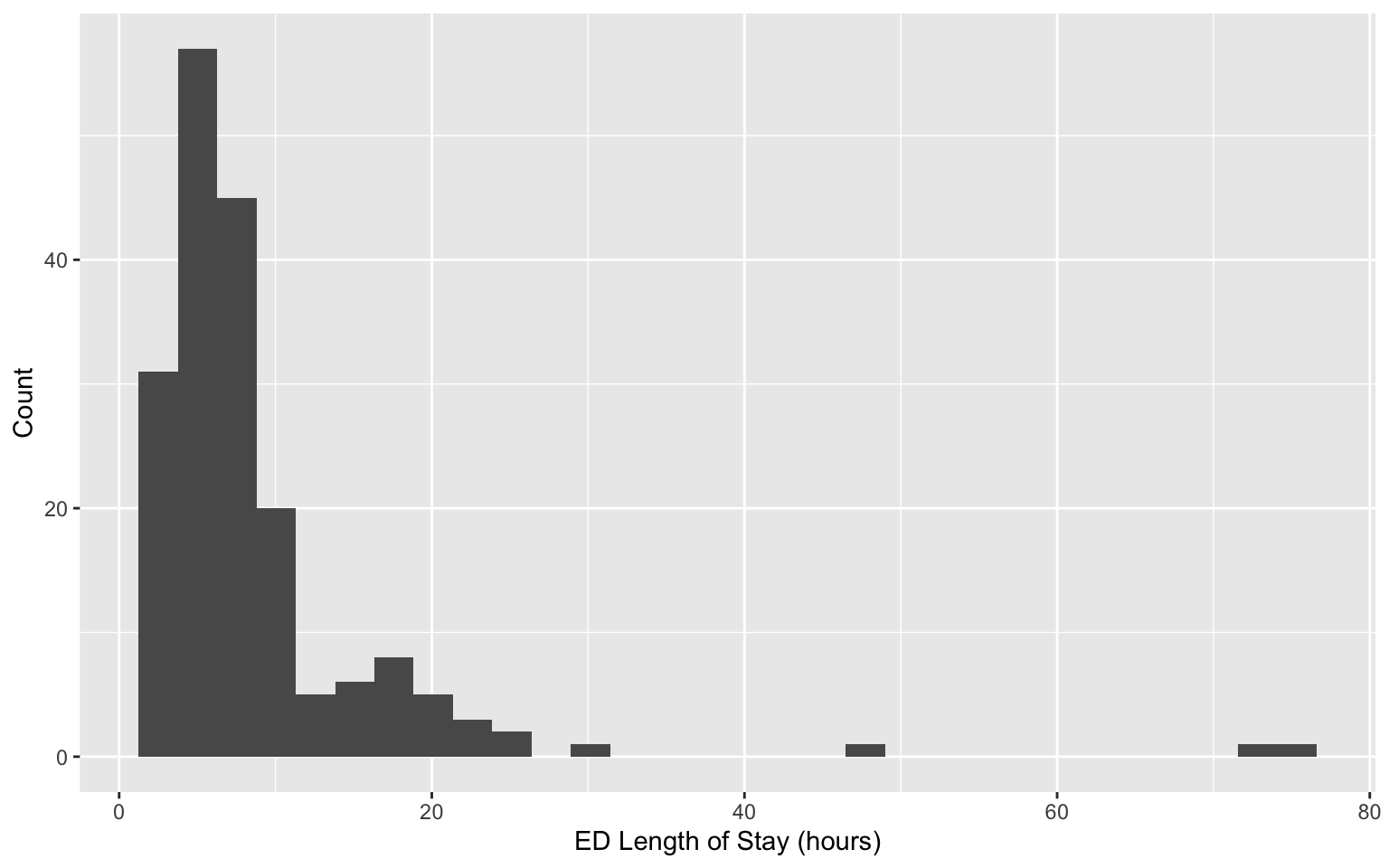
Can we identify subgroups within this population?
The usual setup
Most models introduced in this course are of the form:
The usual setup
Linear regression:
Binary classification:
Limitations of the usual setup
Suppose patients
Limitations of the usual setup
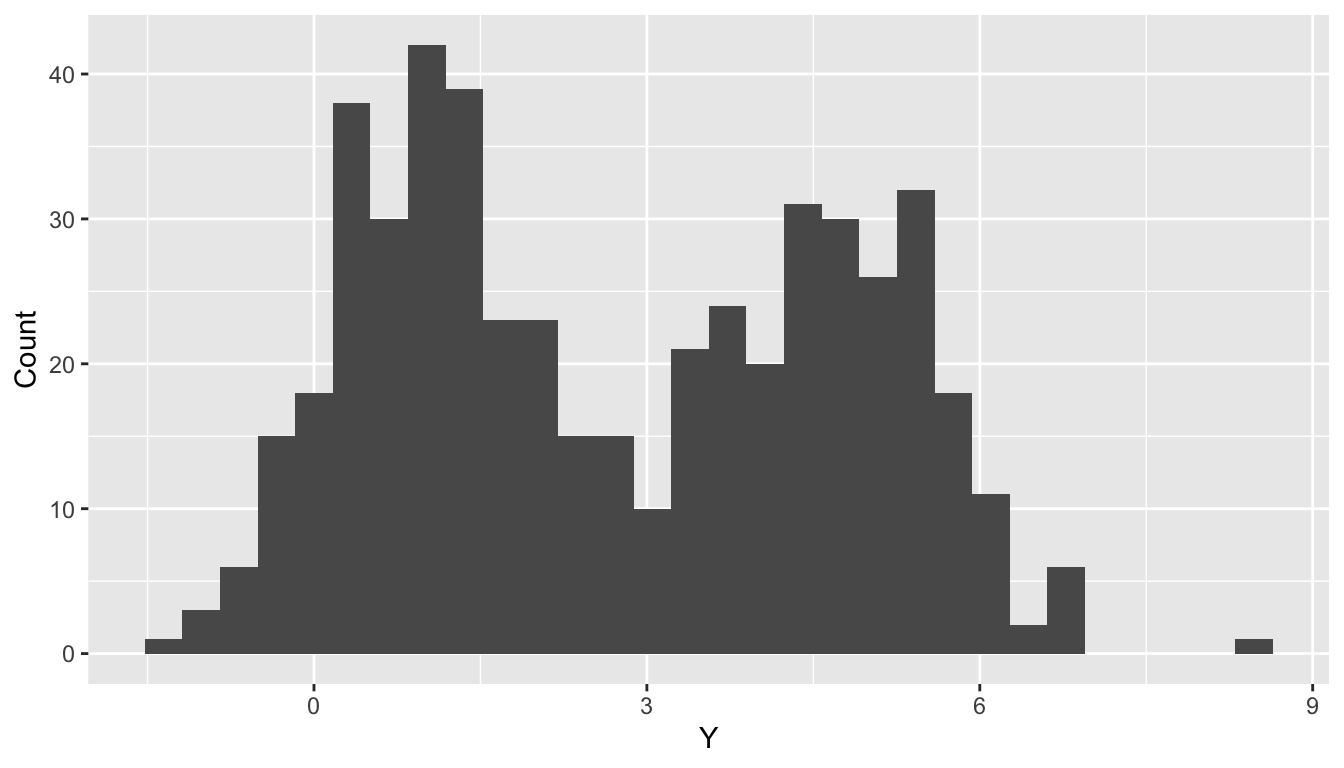
Limitations of the usual setup
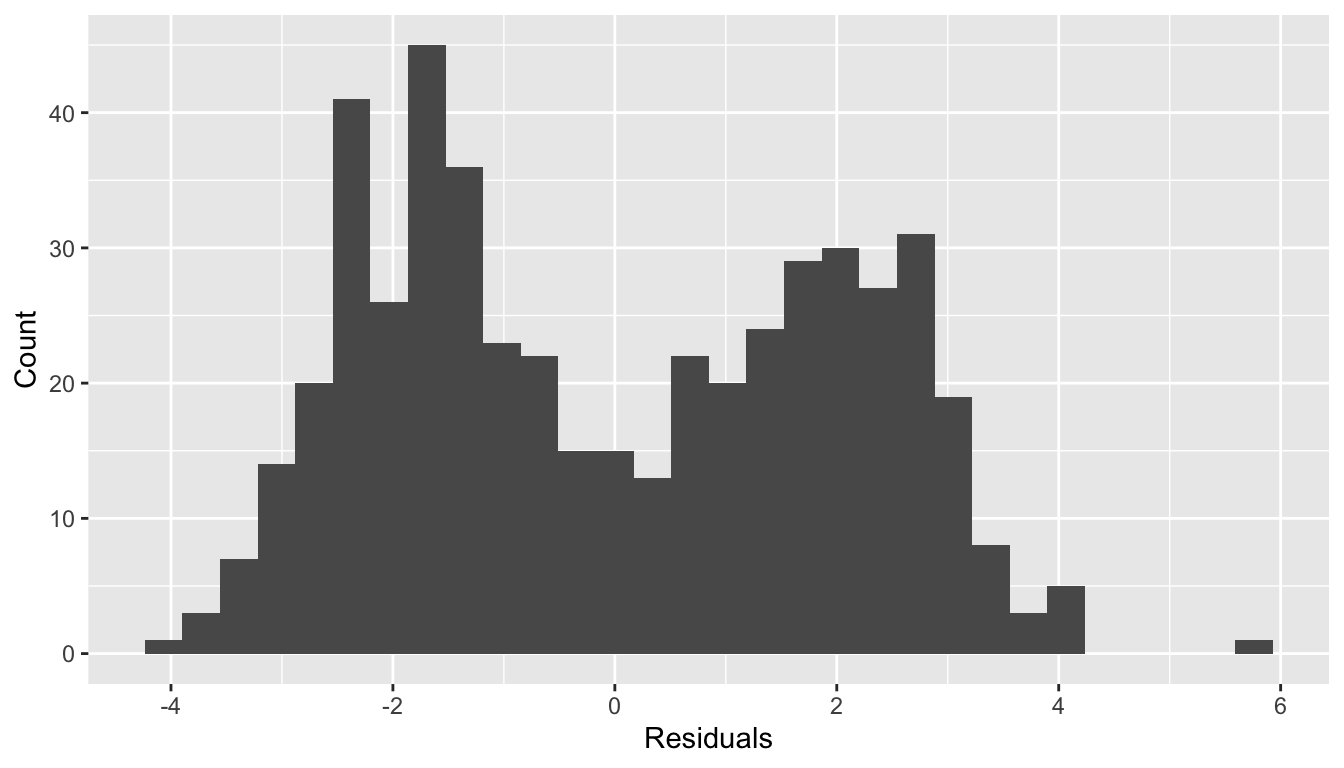
Normality of residuals?
Mixture Model
Motivation for using a mixture model: Standard distributional families are not sufficiently expressive.
- The inflexibility of the model may be due to unobserved heterogeneity (e.g., unrecorded treatment history).
Generically,
Uses of mixture models:
- Modeling weird densities/distributions (e.g., bimodal).
- Learning latent groups/clusters.
Mixture Model
This mixture is comprised of
When
It is common to let,
- The component densities share a functional form and differ in their parameters.
Gaussian Mixture Model
Letting
For multivariate outcomes
Gaussian Mixture Model
Consider a mixture model with 3 groups:
- Mixture 1:
- Mixture 2:
- Mixture 3:
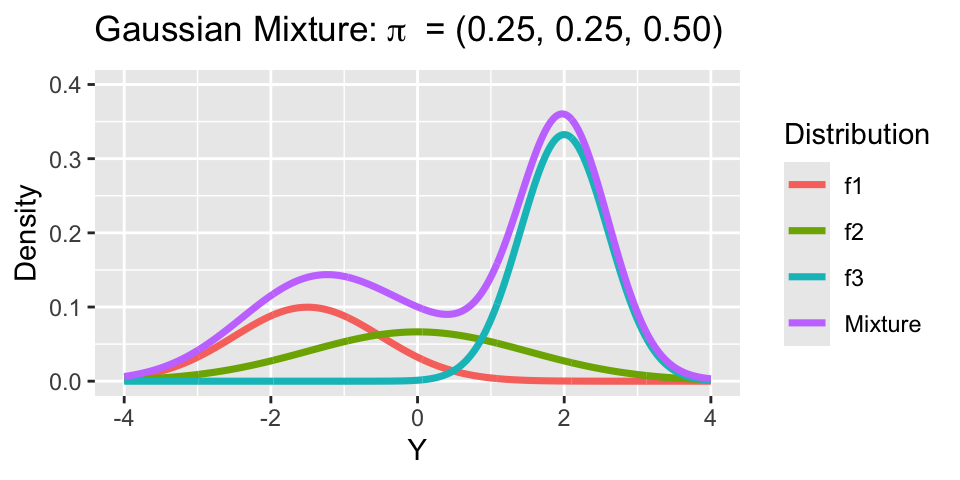
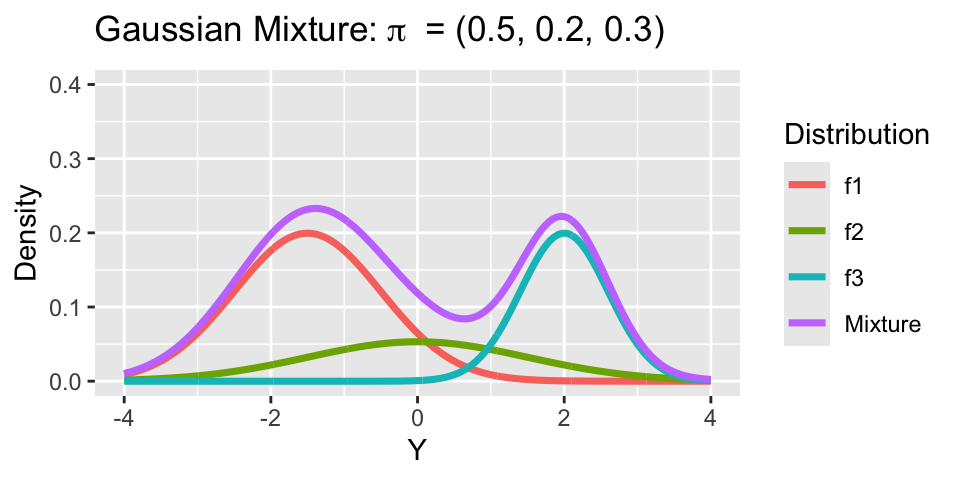
Notice, both means
Generative perspective on GMM
To simulate from a
- Sample the component indicator
- Given
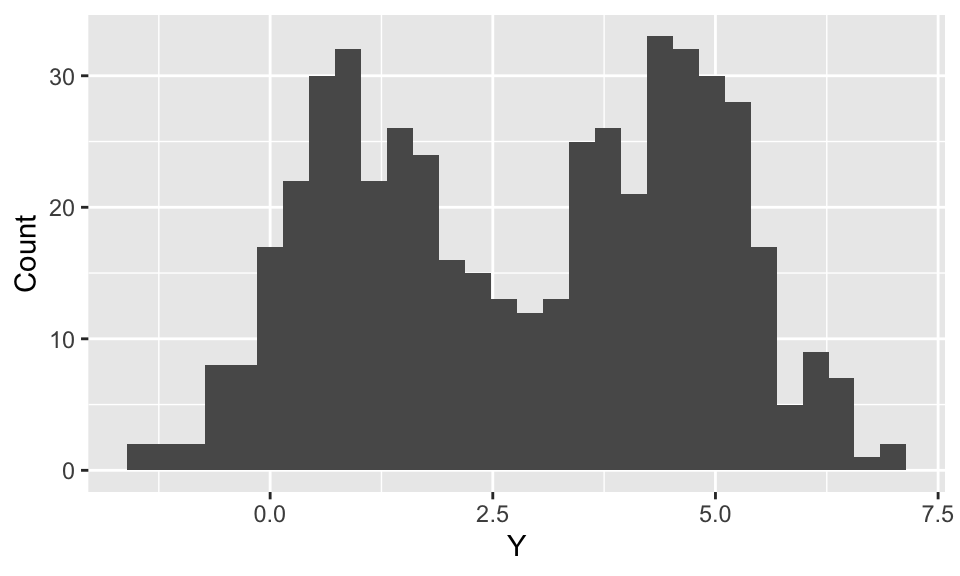
Generative perspective on GMM
This is essentially the code used to simulate the missing treatment history example.
Marginalizing Component Indicators
The label
But
This is key to implementing in Stan.
Gaussian mixture in Stan
Component indicators Stan. As before, suppose
The log-likelihood is:
log_sum_exp is a Stan function.
Gaussian mixture in Stan
// saved in mixture1.stan
data {
int<lower = 1> k; // number of mixture components
int<lower = 1> n; // number of data points
array[n] real Y; // observations
}
parameters {
simplex[k] pi; // mixing proportions
ordered[k] mu; // means of the mixture components
vector<lower=0>[k] sigma; // sds of the mixture components
}
model {
target += normal_lpdf(mu |0.0, 10.0);
target += exponential_lpdf(sigma | 1.0);
vector[k] log_probs = log(pi);
for (i in 1:n){
vector[k] lps = log_probs;
for (h in 1:k){
lps[h] += normal_lpdf(Y[i] | mu[h], sigma[h]);
}
target += log_sum_exp(lps);
}
}Of note: simplex and ordered types.
First fit
Inference for Stan model: anon_model.
4 chains, each with iter=5000; warmup=2500; thin=1;
post-warmup draws per chain=2500, total post-warmup draws=10000.
mean se_mean sd 2.5% 97.5% n_eff Rhat
pi[1] 0.37 0.17 0.24 0.16 0.83 2 6.35
pi[2] 0.63 0.17 0.24 0.17 0.84 2 6.35
mu[1] -3.17 0.09 0.51 -4.49 -2.49 33 1.05
mu[2] 0.45 3.96 5.69 -3.17 13.08 2 5.14
sigma[1] 13.25 4.48 6.46 2.09 20.11 2 4.97
sigma[2] 5.03 3.28 4.68 2.03 14.78 2 7.56
Samples were drawn using NUTS(diag_e) at Sat Mar 22 13:54:38 2025.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).What is going on?
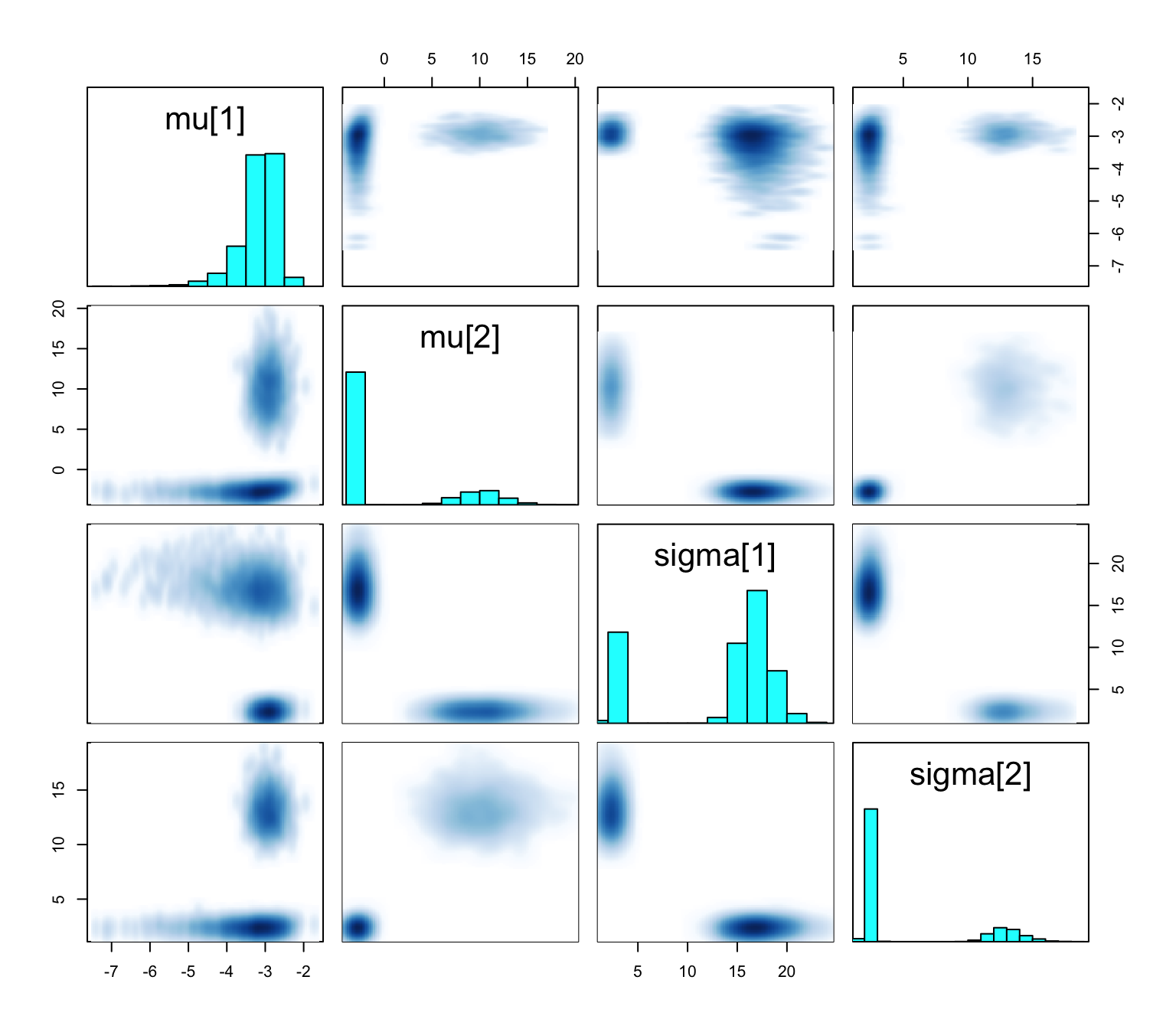
Bimodal posterior
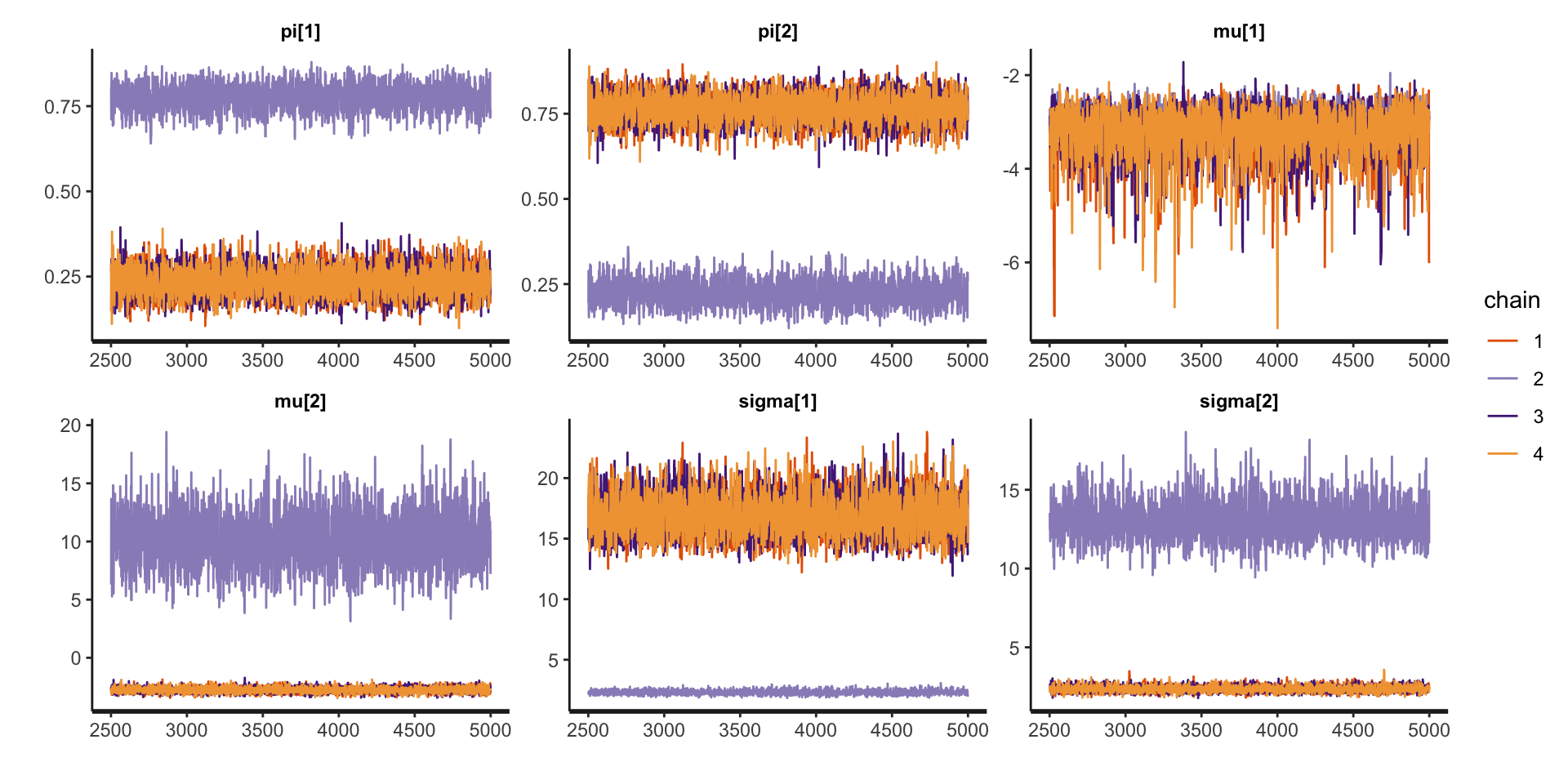
- In one mode,
Bimodal posterior
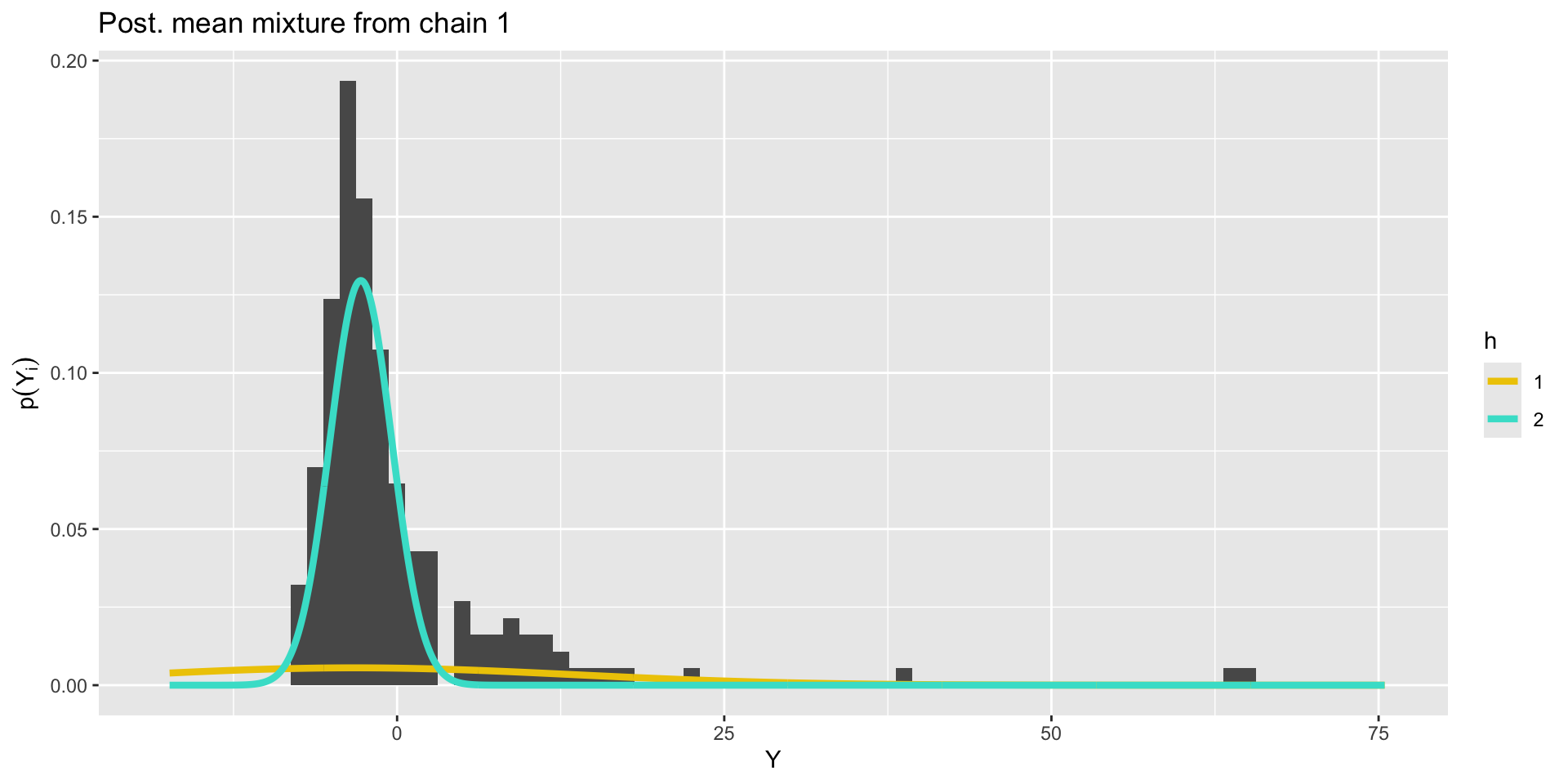
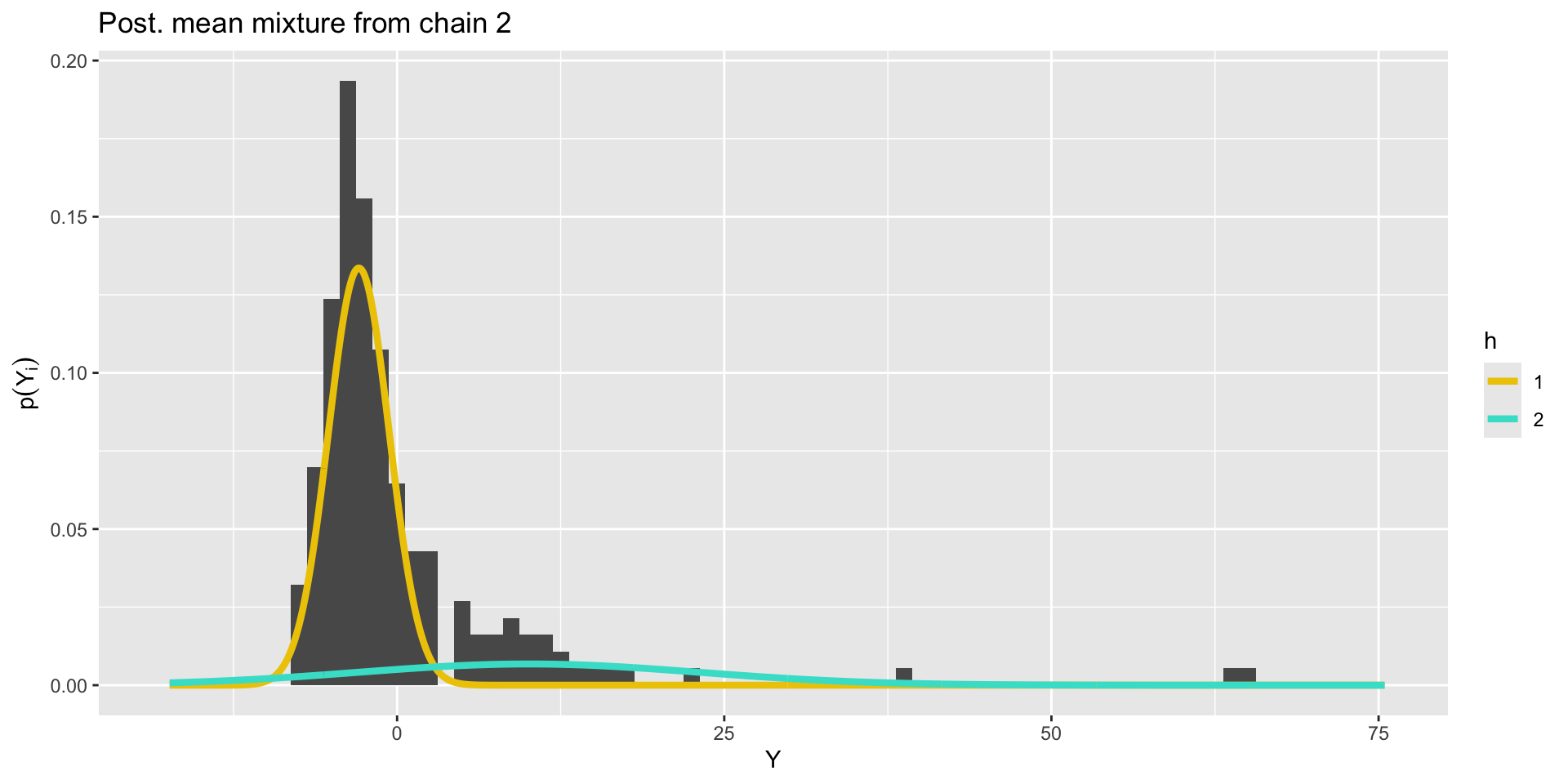
The Gaussian clusters have light tails, so outlying values of
Things to consider when your mixture model is mixed up
Mixture modeling, especially when clusters are of interest, can be fickle.
- Different mixtures can give similar fit to data, leading to multimodal posteriors that are difficult to sample from (previous slides).
- Clusters will depend on your choice of
- Increasing
Things to consider when your mixture model is mixed up
- Employ informative priors.
- Vary the number of clusters.
- Change the form of the kernel.
Updated model
// saved in mixture2.stan
data {
int<lower = 1> k; // number of mixture components
int<lower = 1> n; // number of data points
array[n] real Y; // observations
}
parameters {
simplex[k] pi; // mixing proportions
ordered[k] mu; // means of the mixture components
vector<lower = 0>[k] sigma; // sds of the mixture components
vector<lower = 1>[k] nu;
}
model {
target += normal_lpdf(mu | 0.0, 10.0);
target += normal_lpdf(sigma | 2.0, 0.5);
target += gamma_lpdf(nu | 5.0, 0.5);
vector[k] log_probs = log(pi);
for (i in 1:n){
vector[k] lps = log_probs;
for (h in 1:k){
lps[h] += student_t_lpdf(Y[i] | nu[h], mu[h], sigma[h]);
}
target += log_sum_exp(lps);
}
}- Informative prior on
- Mixture of Student-t.
Updated model fit
Inference for Stan model: anon_model.
4 chains, each with iter=5000; warmup=2500; thin=1;
post-warmup draws per chain=2500, total post-warmup draws=10000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
pi[1] 0.81 0.00 0.04 0.73 0.79 0.81 0.83 0.87 5567 1
pi[2] 0.19 0.00 0.04 0.13 0.17 0.19 0.21 0.27 5567 1
mu[1] -2.96 0.00 0.22 -3.39 -3.10 -2.96 -2.81 -2.53 7318 1
mu[2] 8.30 0.02 1.10 6.03 7.66 8.35 9.01 10.28 4306 1
sigma[1] 2.20 0.00 0.17 1.88 2.09 2.20 2.31 2.55 5987 1
sigma[2] 2.82 0.00 0.40 2.06 2.55 2.81 3.09 3.64 6745 1
nu[1] 11.98 0.04 4.44 5.14 8.75 11.38 14.57 22.22 9860 1
nu[2] 1.54 0.00 0.43 1.03 1.25 1.46 1.74 2.50 9286 1
Samples were drawn using NUTS(diag_e) at Sat Mar 29 12:52:38 2025.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).Updated model results
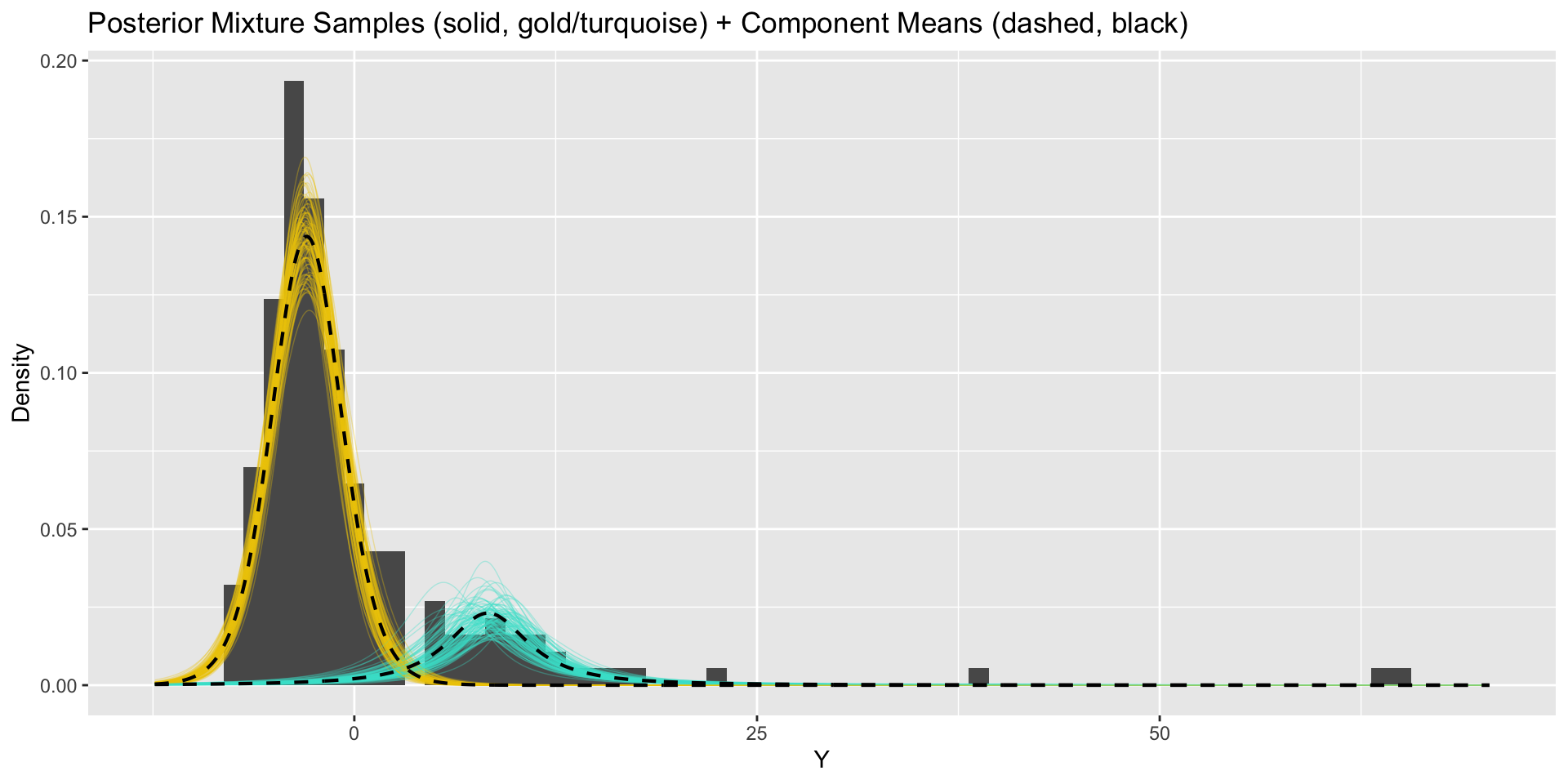
From marginal mixture model to clusters
Stan cannot directly infer categorical component indicators
Given these cluster membership probabilities, we can recover cluster indicators through simulation:
From marginal mixture model to clusters
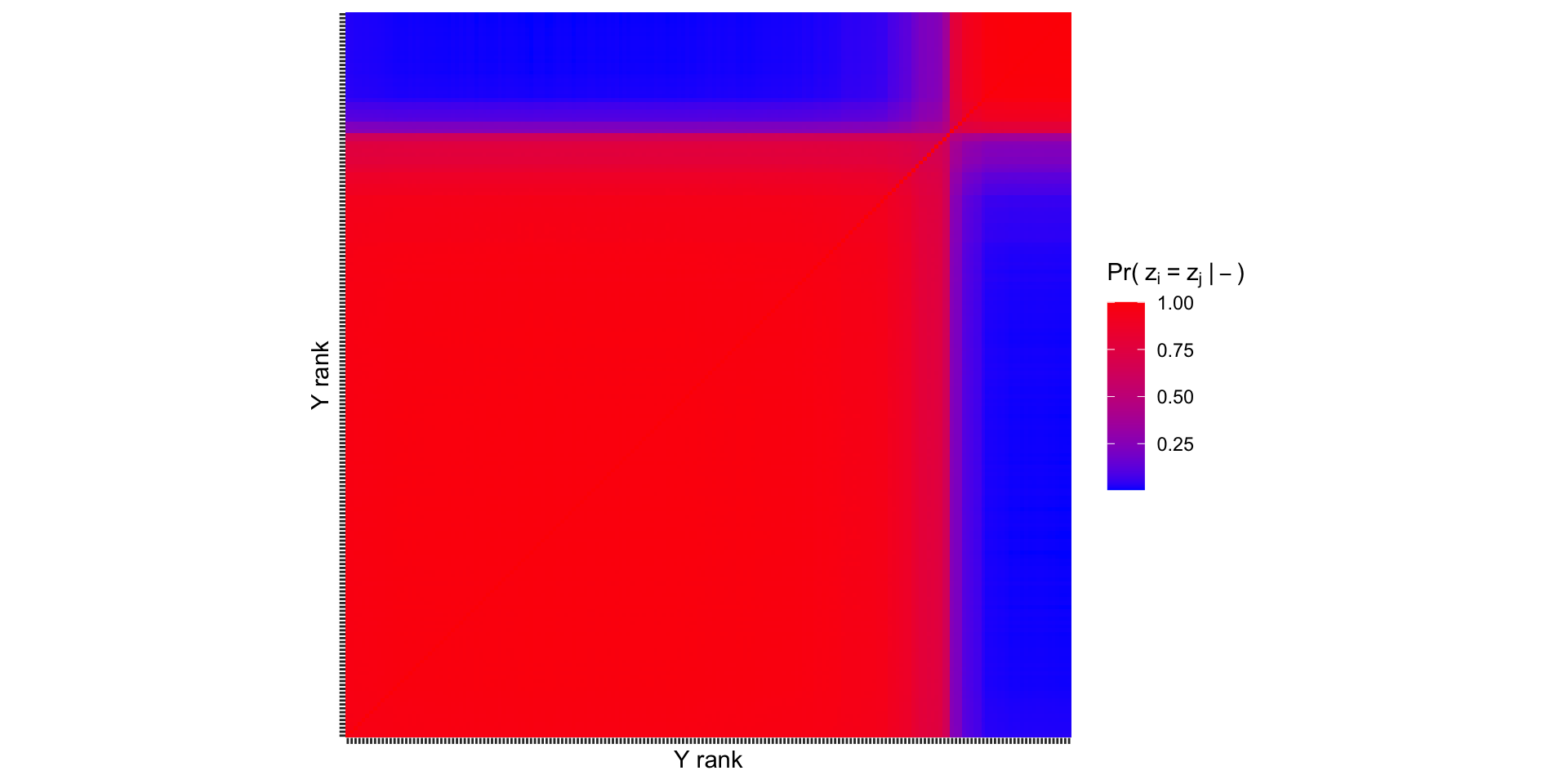
Co-clustering probabilities
Recovering
It is common to arrange these probabilities in a co-clustering matrix
Co-clustering probabilities
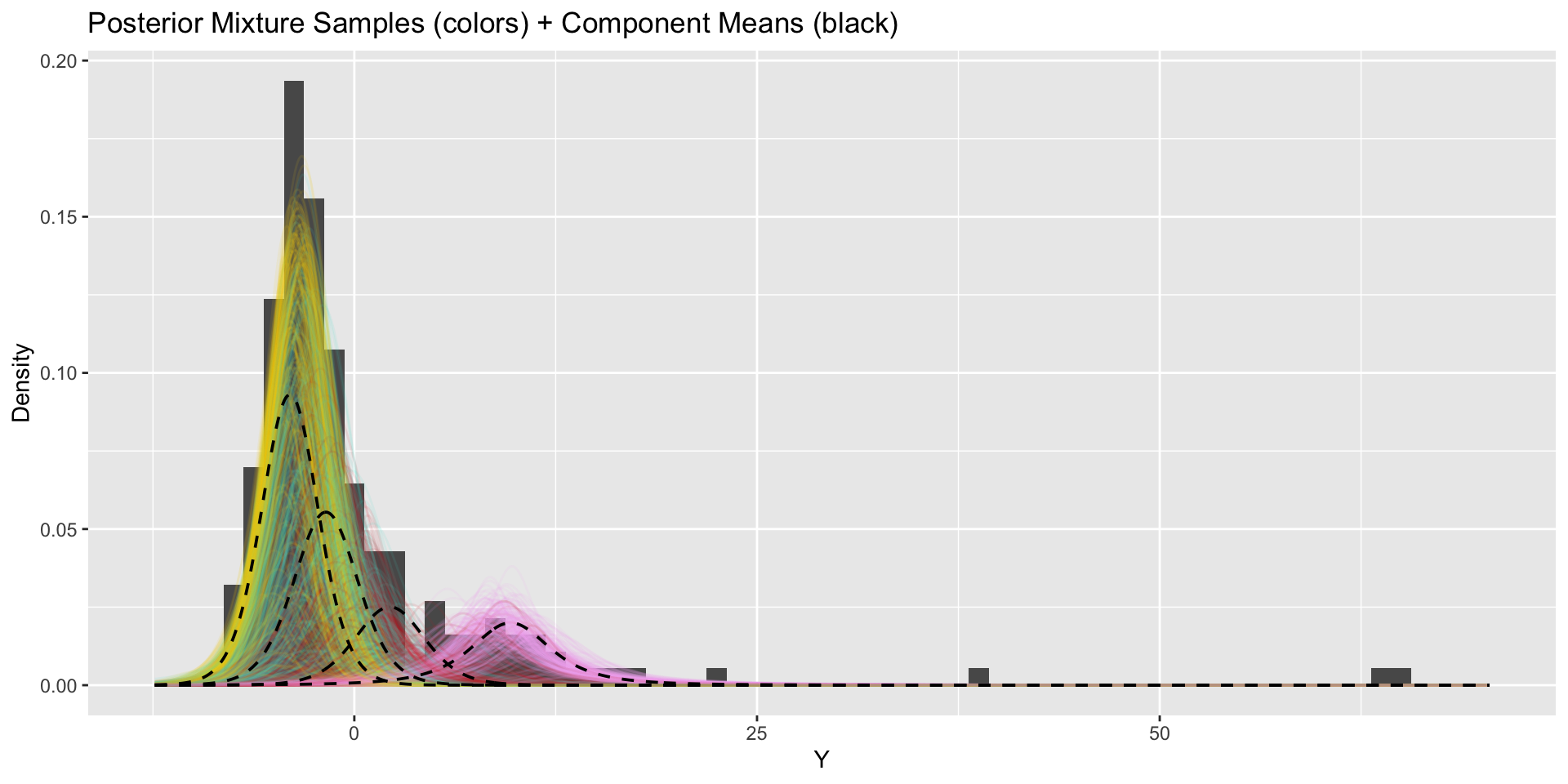
How do our results change when we use more components?
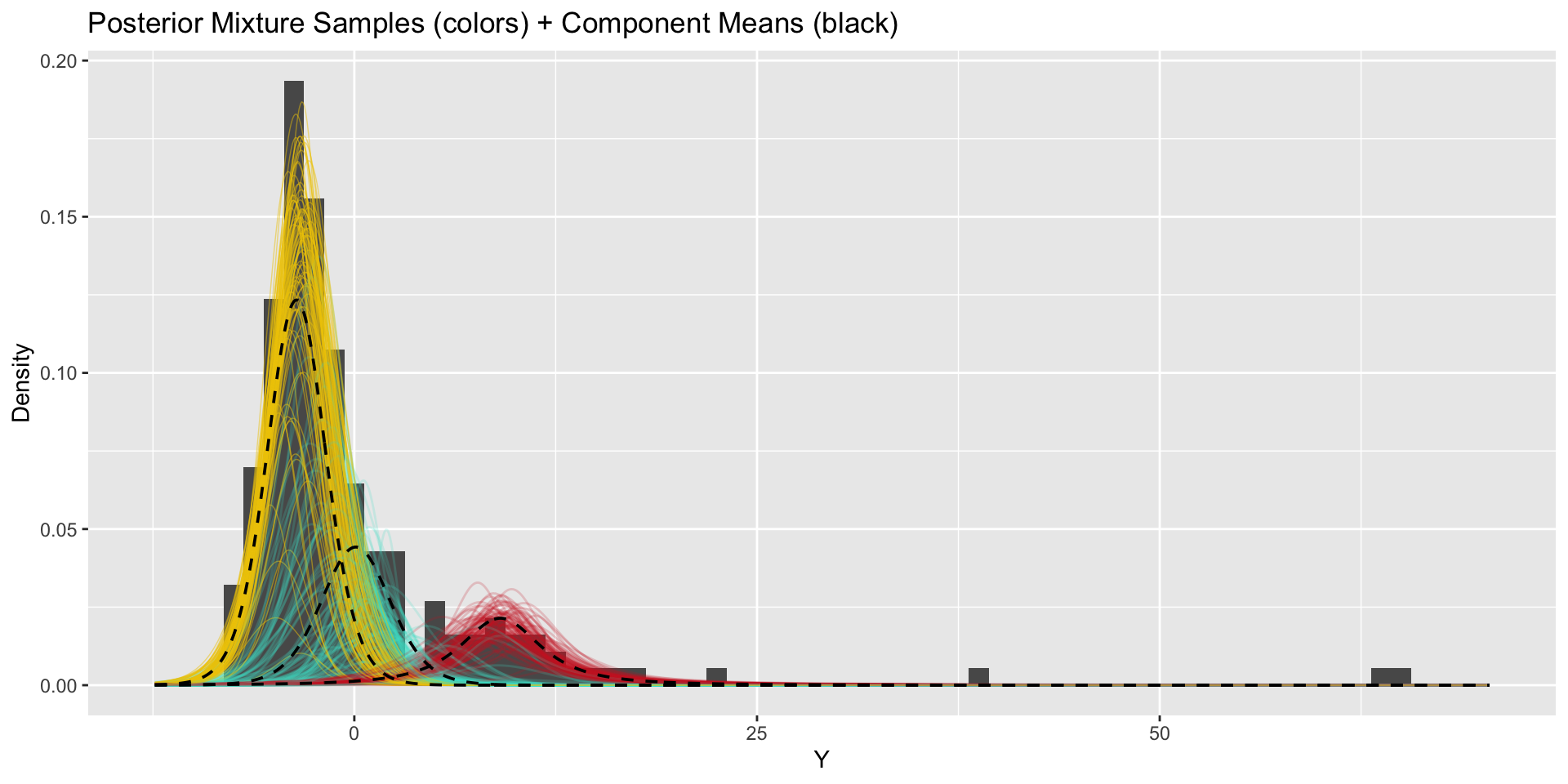
How do our results change when we use more components?
Co-clusterings across
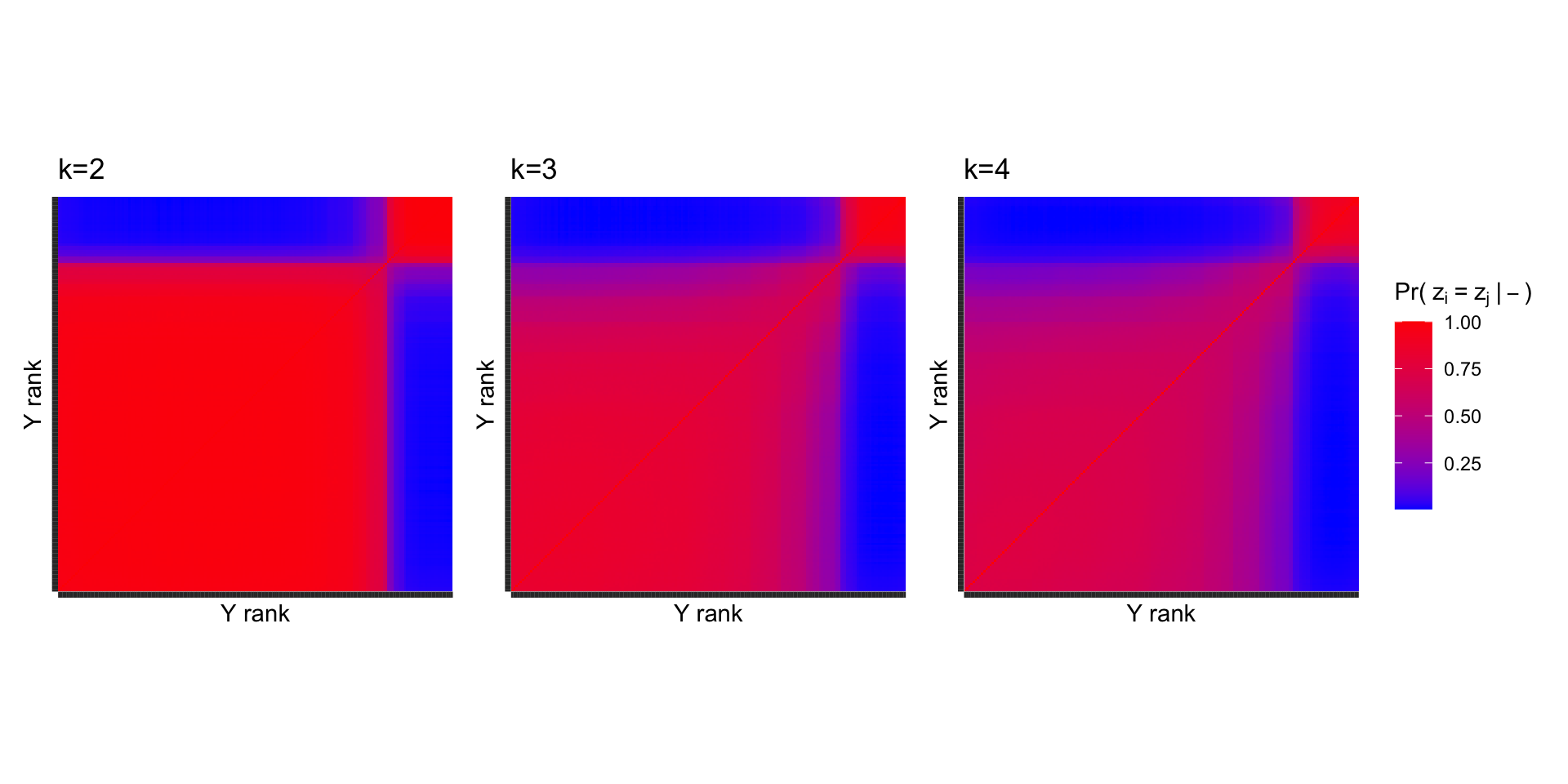
The same general pattern persists when more clusters are used, indicating that
Characterizing the Clusters
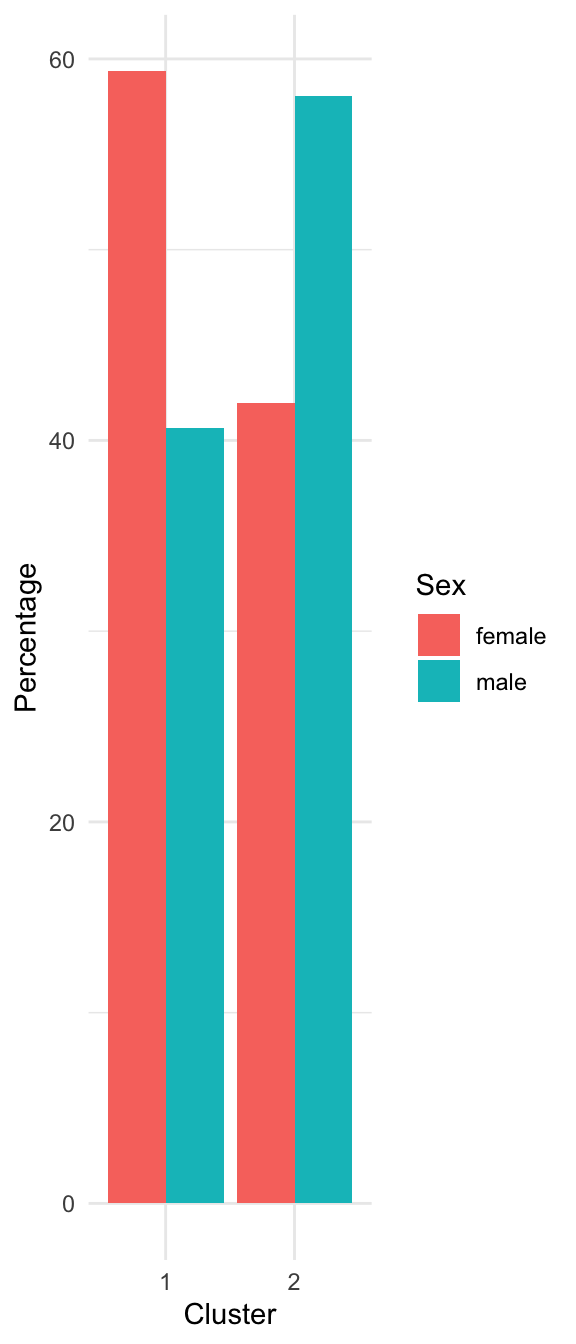
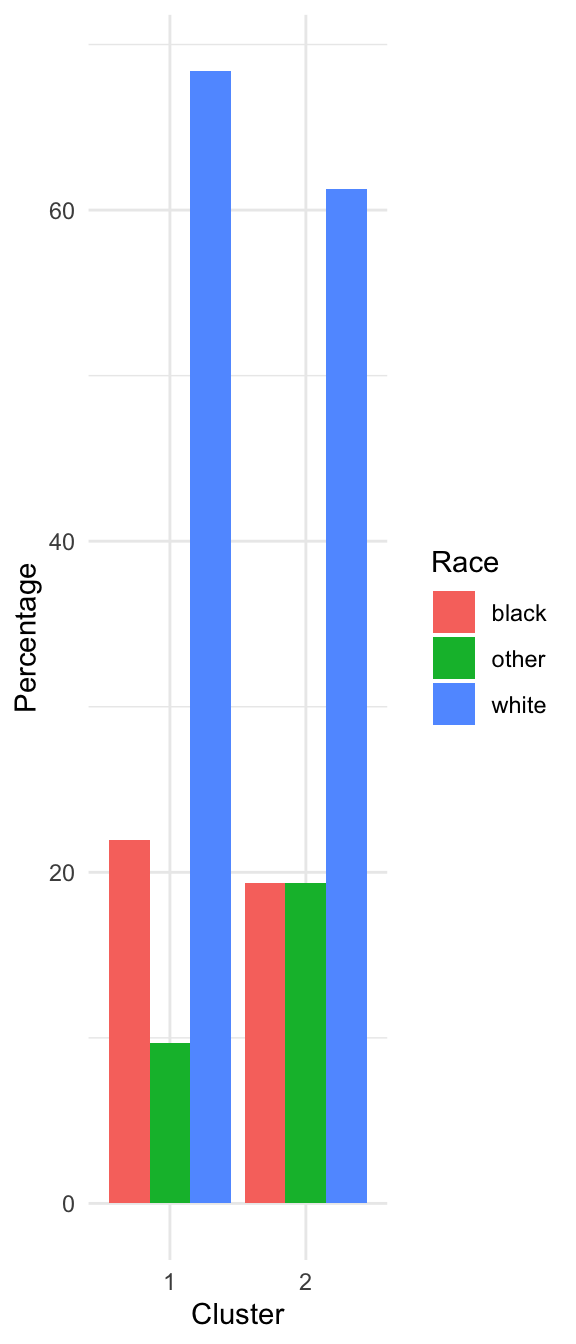
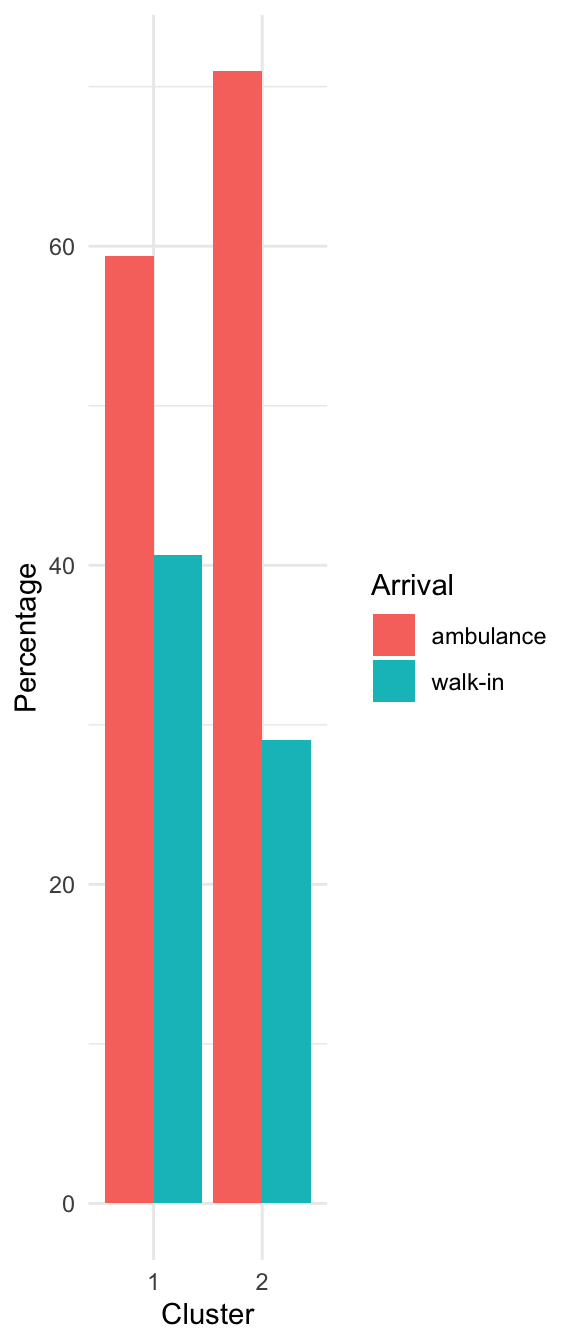
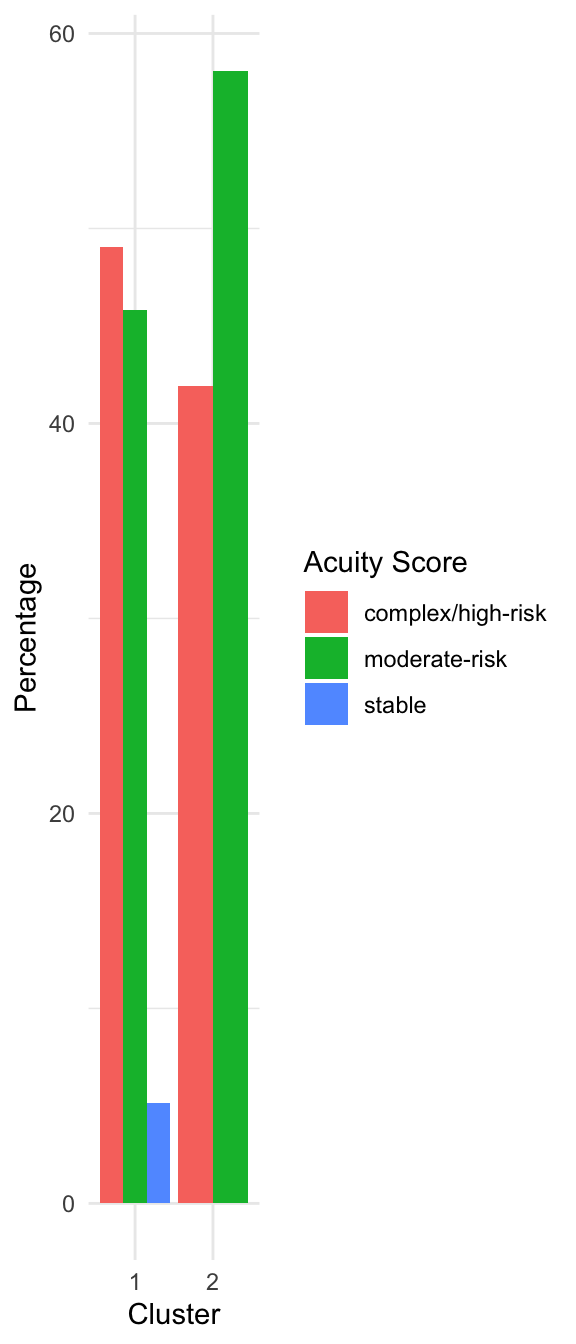
Characterizing the Clusters
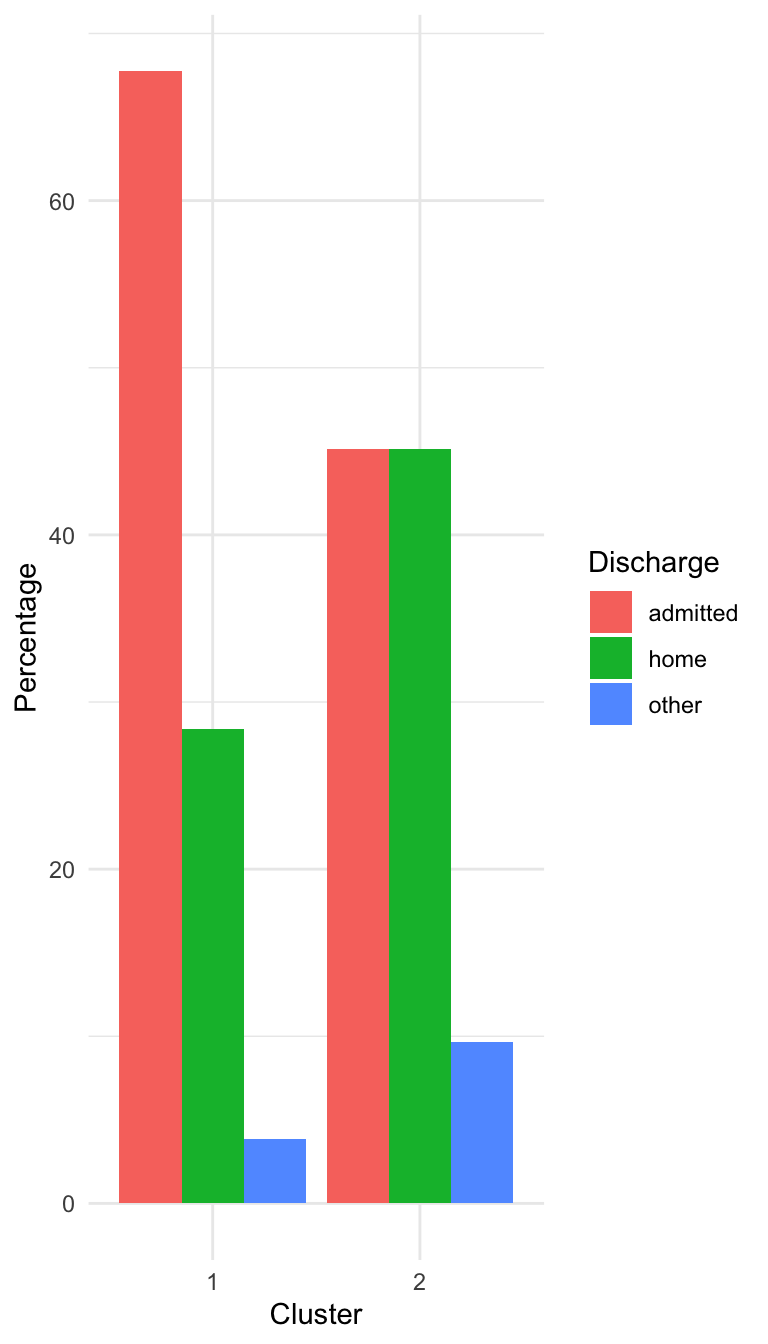
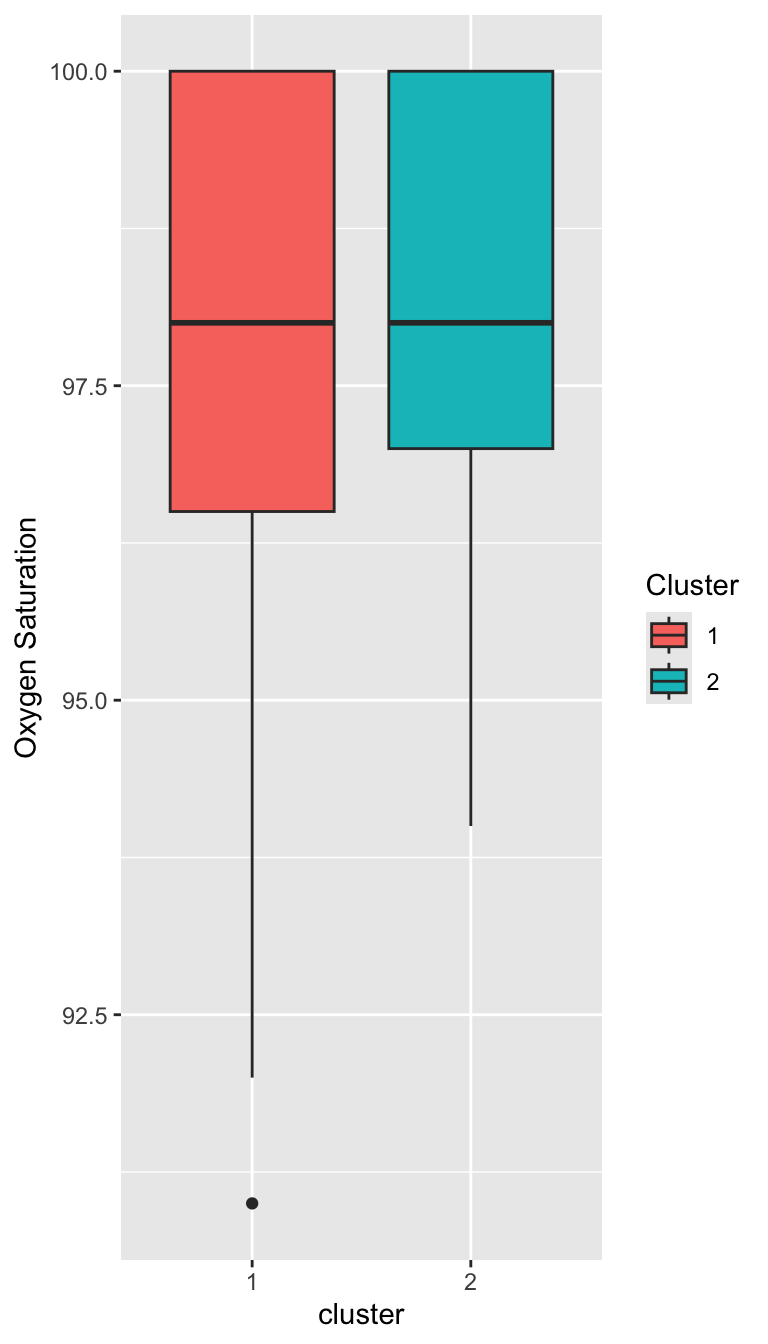
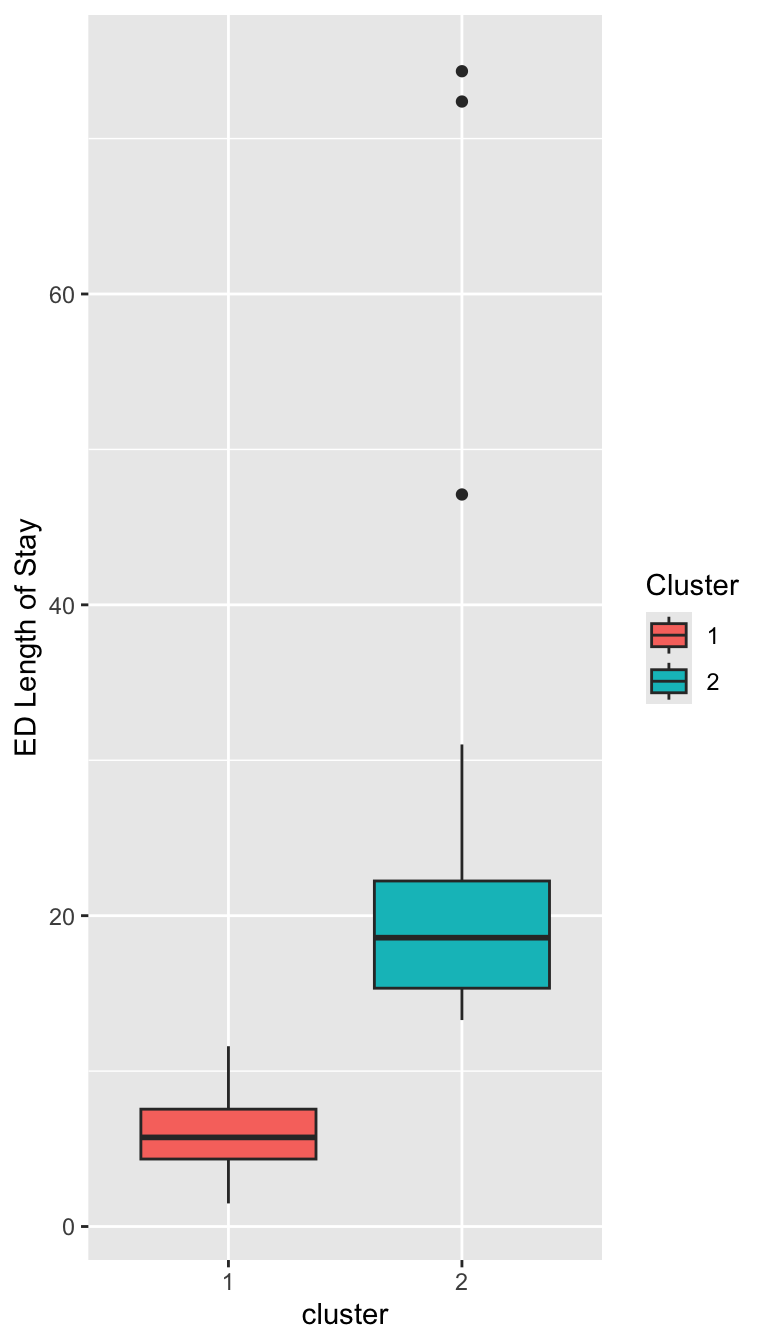
Prepare for next class
Reminder: On Thursday, we will have a in-class live-coding exercise.
Begin working on Exam 02, which is due for feedback on April 15.