IgG Age
1 1.5 0.5
2 2.7 0.5
3 1.9 0.5
4 4.0 0.5
5 1.9 0.5
6 4.4 0.5Robust Regression
Feb 11, 2025
Review of last lecture
On Thursday, we started to branch out from linear regression.
We learned about approaches for nonlinear regression.
Today we will address approaches for robust regression, which will generalize the assumption of homoskedasticity (and also the normality assumption).
A motivating research question
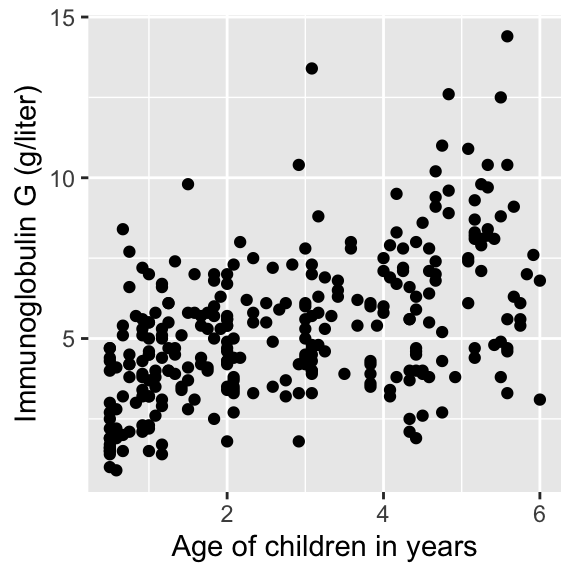
In today’s lecture, we will look at data on serum concentration (grams per litre) of immunoglobulin-G (IgG) in 298 children aged from 6 months to 6 years.
- A detailed discussion of this data set may be found in Isaacs et al. (1983) and Royston and Altman (1994).
For an example patient, we define
Pulling the data
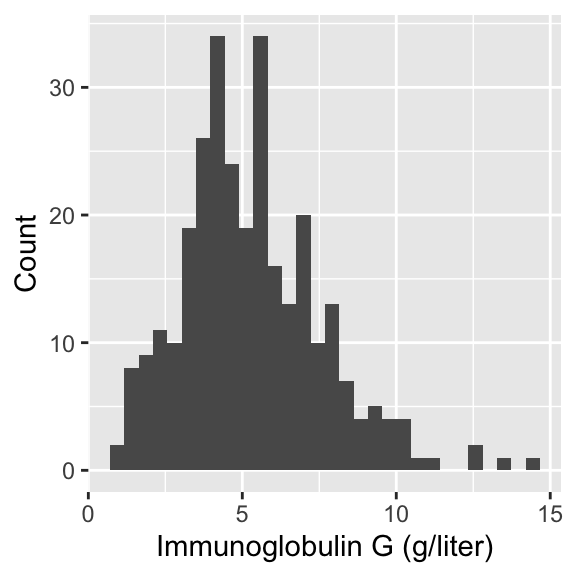
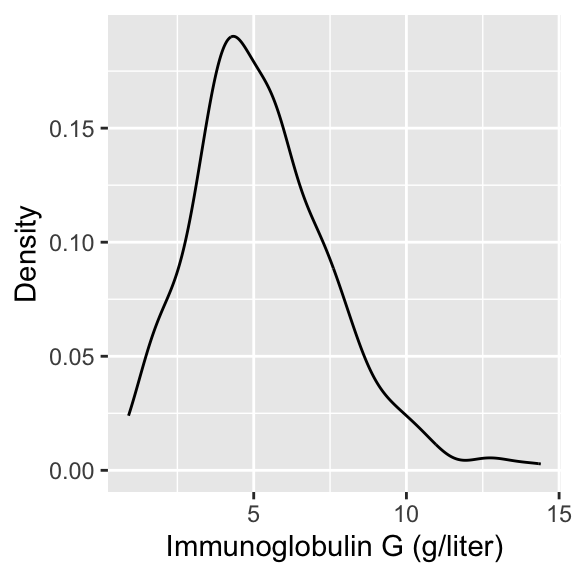
Visualizing IgG data
Modeling the association between age and IgG
- Linear regression can be written as follows for
Linear regression assumptions
Assumptions:
Assessing assumptions
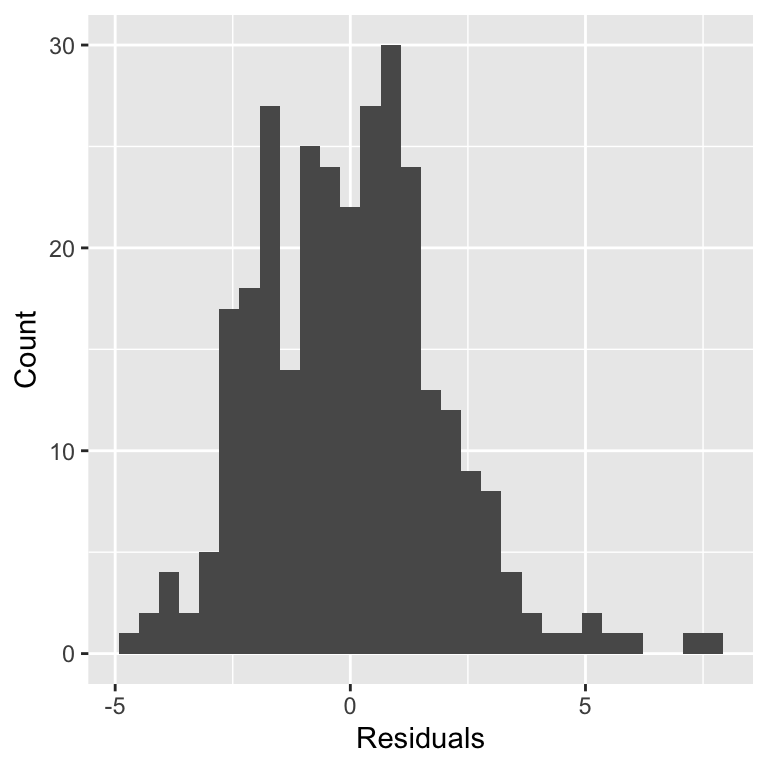
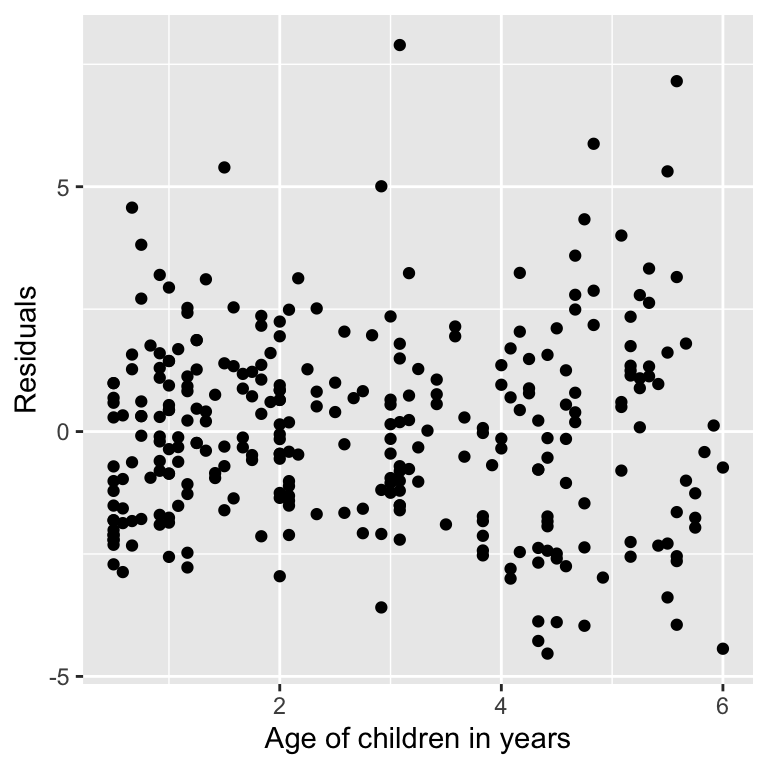
Robust regression
Today we will learn about regression techniques that are robust to the assumptions of linear regression.
We will introduce the idea of robust regression by exploring ways to generalize the homoskedastic variance assumption in linear regression.
We will touch on heteroskedasticity, heavy-tailed distributions, and median regression (more generally quantile regression).
Why is robust regression not more comomon?
Despite their desirable properties, robust methods are not widely used. Why?
Historically computationally complex.
Not available in statistical software packages.
Bayesian modeling using Stan alleviates these bottlenecks!
Heteroskedasticity
Heteroskedasticity is the violation of the assumption of constant variance.
How can we handle this?
In OLS, there are approaches like heteroskedastic consistent errors, but this is not a generative model.
In the Bayesian framework, we generally like to write down generative models.
Modeling the scale with covariates
One option is to allow the sale to be modeled as a function of covariates.
It is common to model the log-transformation of the scale or variance to transform it to
where
Other options include:
Other options include:
Any plausible generative model can be specified!
Modeling the scale with covariates
Heteroskedastic variance
We can write the regression model using a observation specific variance,
One way of writing the variance is:
In the Bayesian framework, we must place a prior on
A prior to induce a heavy-tail
- A common prior for
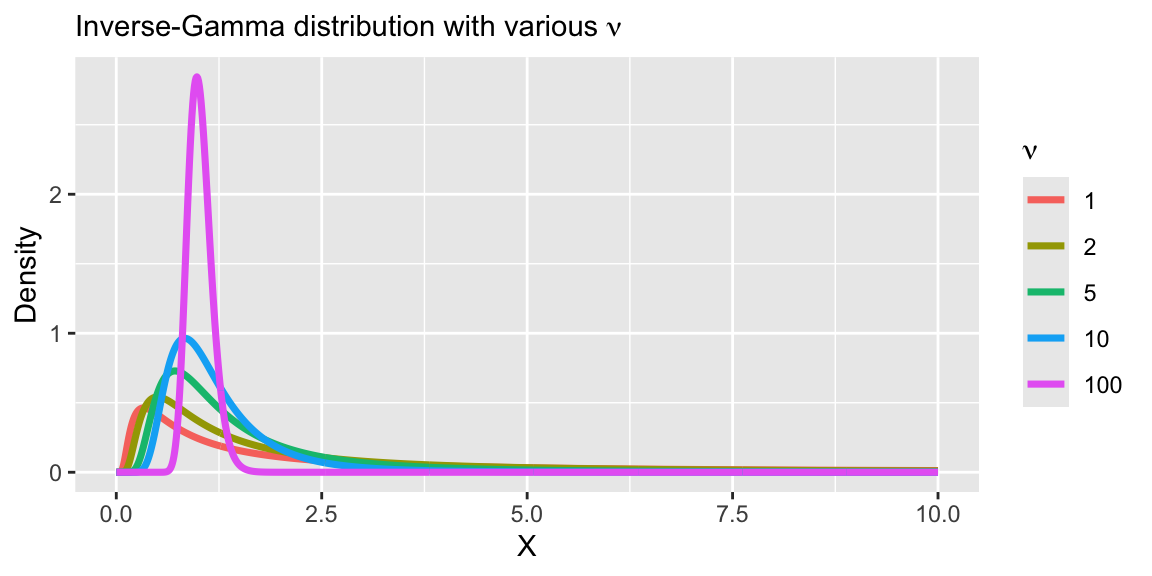
A prior to induce a heavy-tail
- A common prior for
- Under this prior, the marginal likelihood for
Understanding the equivalence
- Heteroskedastic variances assumption is equivalent to assuming a heavy-tailed distribution.
- Note that since the number of
Understanding the equivalence
- The marginal likelihood can be viewed as a mixture of a Gaussian likelihood with an Inverse-Gamma scale parameter.
Understanding the equivalence
A random variable
- We then have:
Student-t in Stan
Student-t in Stan: mixture
data {
int<lower = 1> n;
int<lower = 1> p;
vector[n] Y;
matrix[n, p] X;
}
parameters {
real alpha;
vector[p] beta;
real<lower = 0> sigma;
vector[n] lambda;
real<lower = 0> nu;
}
transformed parameters {
vector[n] tau = sigma * sqrt(lambda);
}
model {
target += normal_lpdf(Y | alpha + X * beta, tau);
target += inv_gamma_lpdf(lambda | 0.5 * nu, 0.5 * nu);
}Why heavy-tailed distributions?
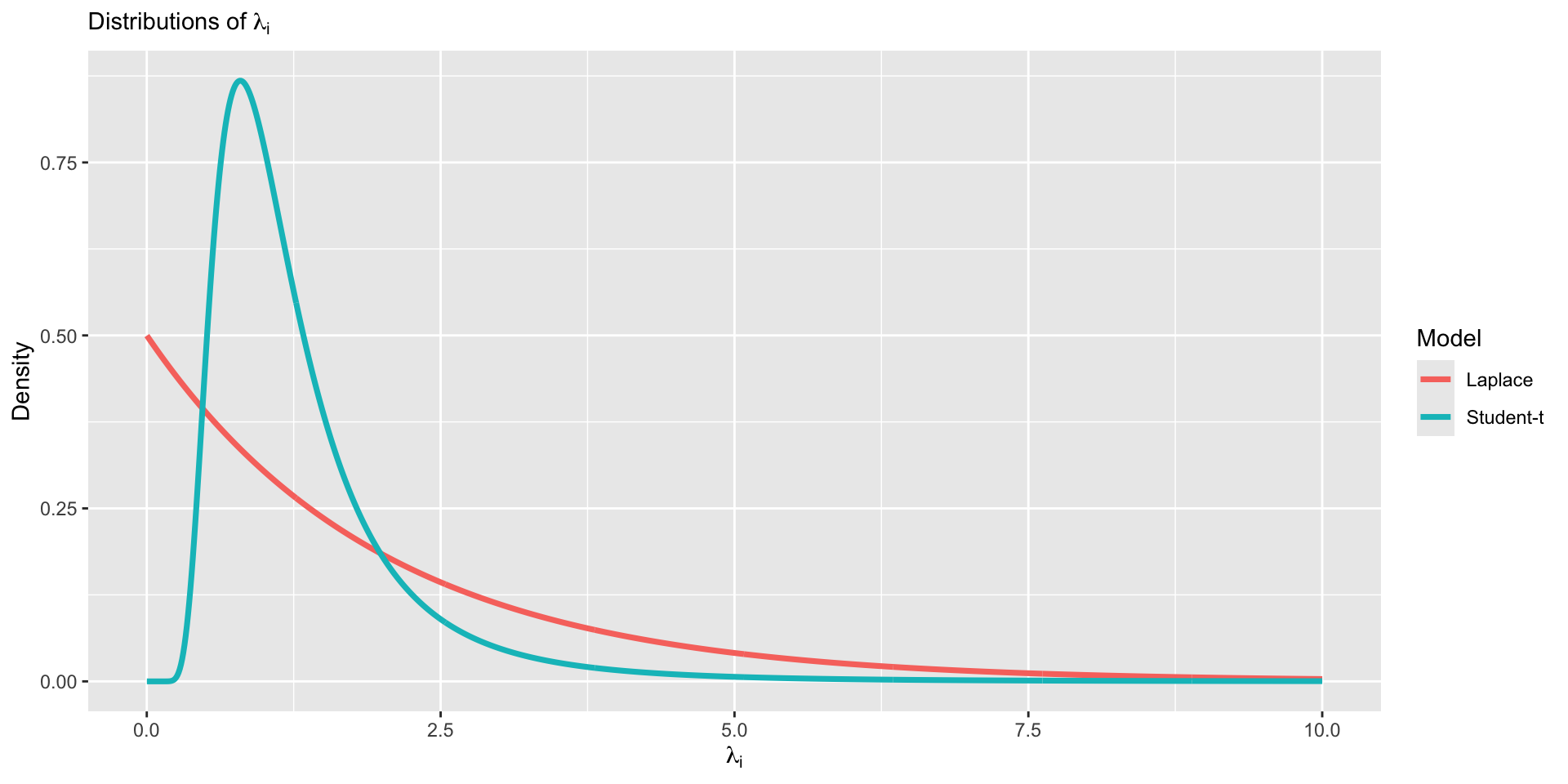
Replacing the normal distribution with a distribution with heavy-tails (e.g., Student-t, Laplace) is a common approach to robust regression.
Robust regression refers to regression methods which are less sensitive to outliers or small sample sizes.
Linear regression, including Bayesian regression with normally distributed errors is sensitive to outliers, because the normal distribution has narrow tail probabilities.
Our heteroskedastic model that we just explored is only one example of a robust regression model.
Vizualizing heavy tail distributions
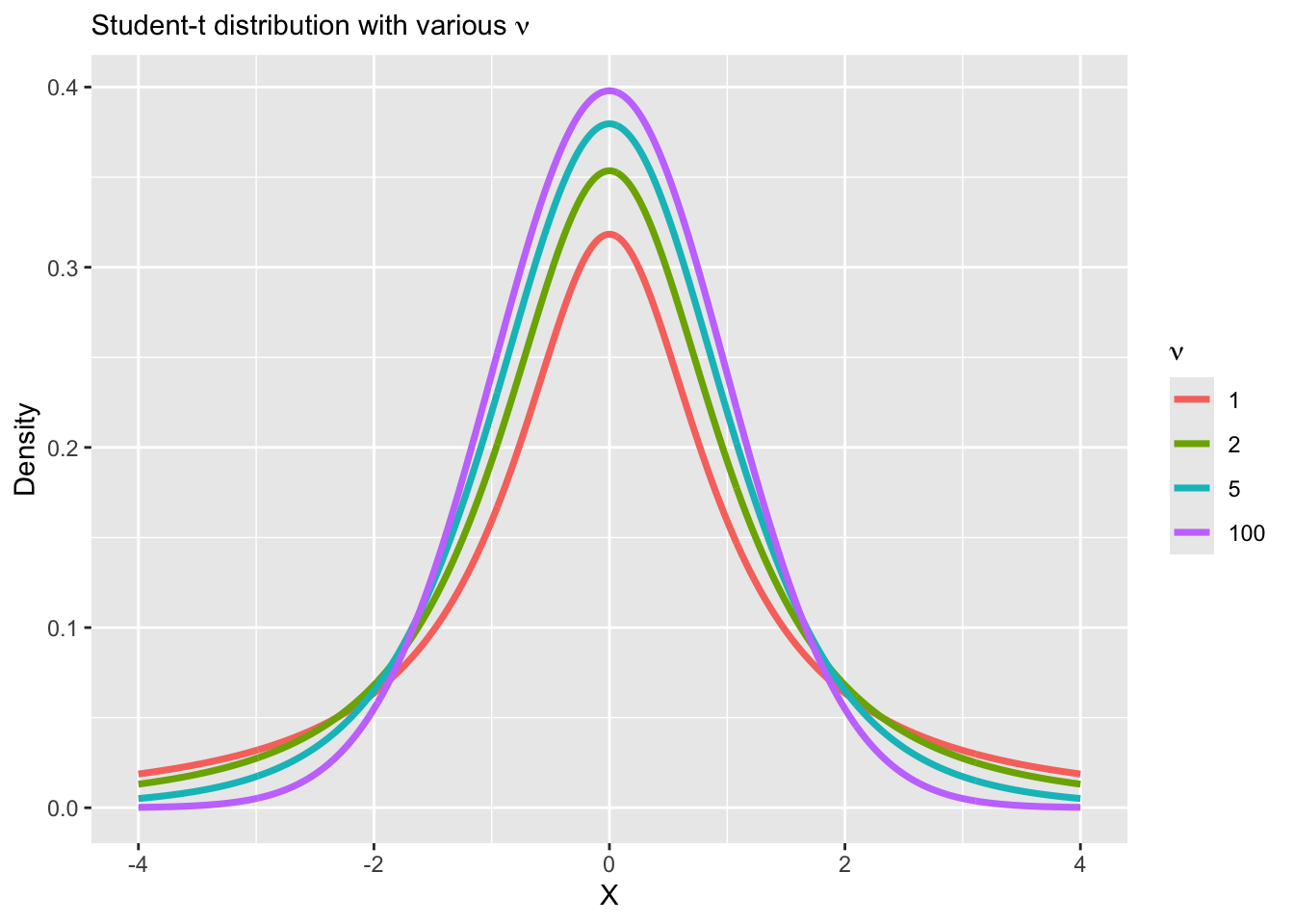
Vizualizing heavy tail distributions
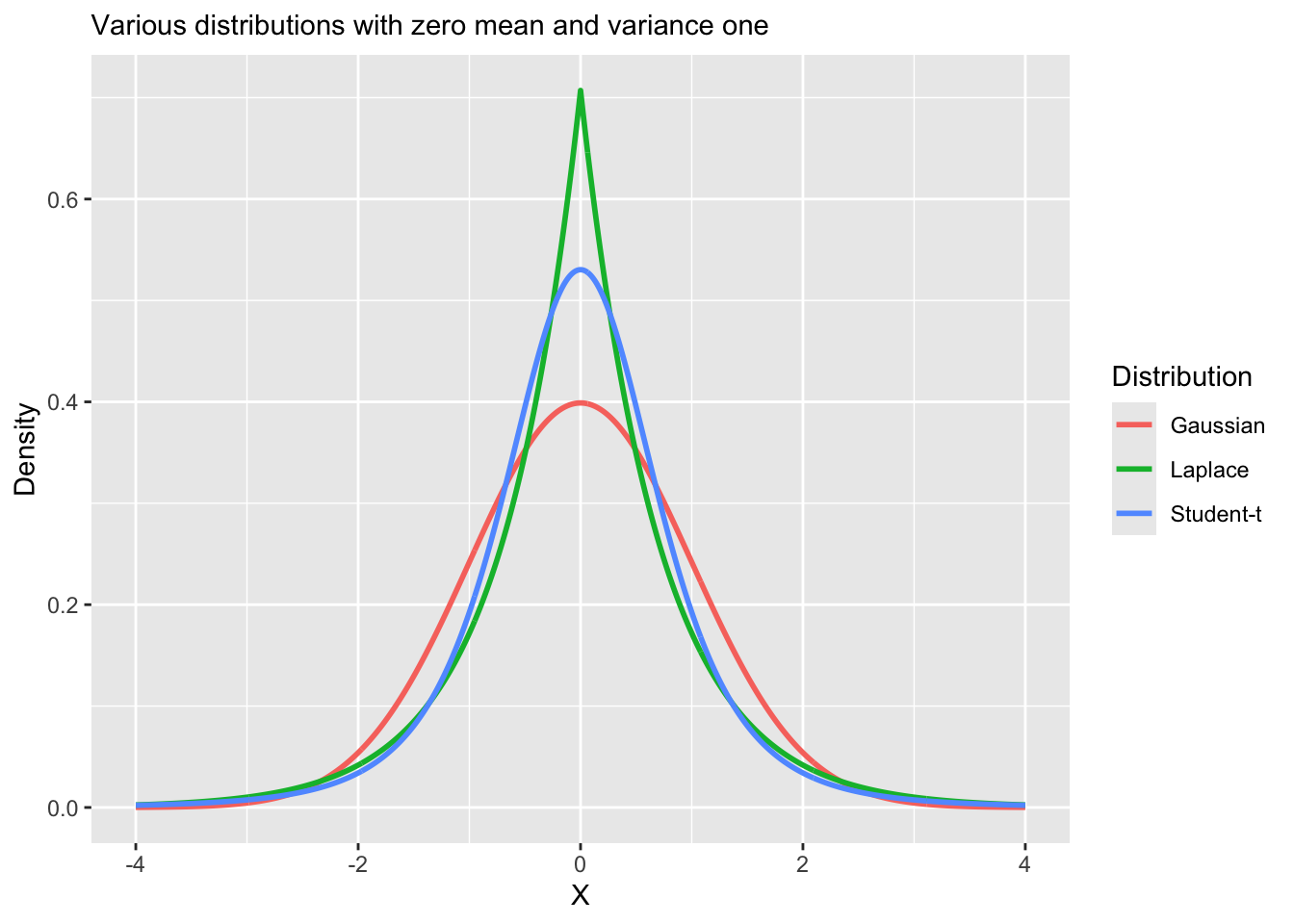
Vizualizing heavy tail distributions
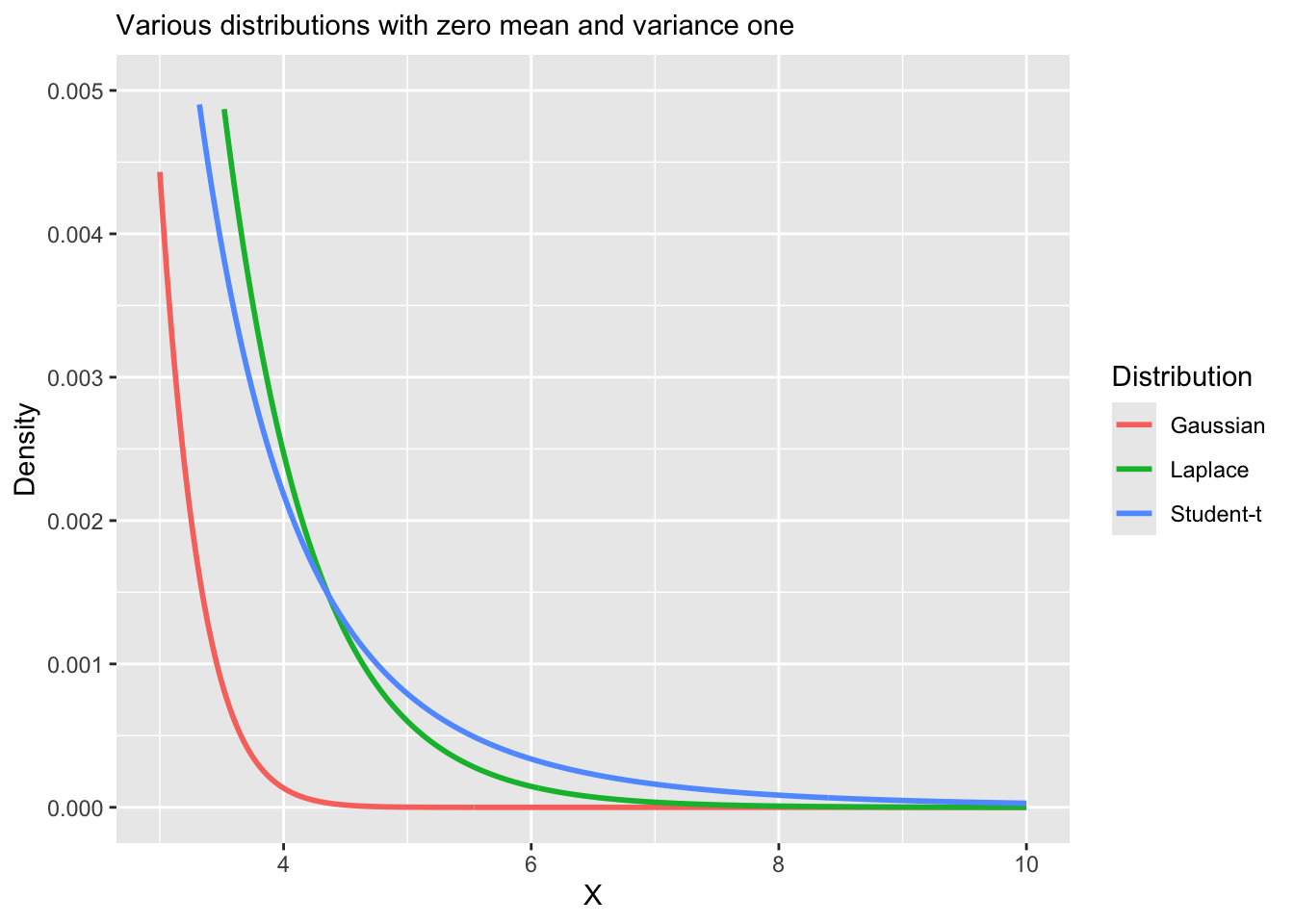
Another example of robust regression
Let’s revisit our general heteroskedastic regression,
We can induce another form of robust regression using the following prior for
Another example of robust regression
Let’s revisit our general heteroskedastic regression,
We can induce another form of robust regression using the following prior for
Under this prior, the induced marginal model is,
This has a really nice interpretation!
Laplace distribution
Suppse a variable
Under the Laplace likelihood, estimation of
Median regression using Laplace
Least absolute deviation (LAD) regression minimizes the following objective function,
The Bayesian analog is the Laplace distribution,
Median regression using Laplace
The Laplace distribution is analogous to least absolute deviations because the kernel of the distribution is
Laplace distribution is also known as the double-exponential distribution (symmetric exponential distributions around
Thus, a linear regression with Laplace errors is analogous to a median regression,
Why is median regression considered more robust than regression of the mean?
Laplace regression in Stan
Laplace regression in Stan: mixture
data {
int<lower = 1> n;
int<lower = 1> p;
vector[n] Y;
matrix[n, p] X;
}
parameters {
real alpha;
vector[p] beta;
real<lower = 0> sigma;
vector[n] lambda;
}
transformed parameters {
vector[n] tau = sigma * sqrt(lambda);
}
model {
target += normal_lpdf(Y | alpha + X * beta, tau);
target += exponential_lpdf(lambda | 0.5);
}Returning to IgG
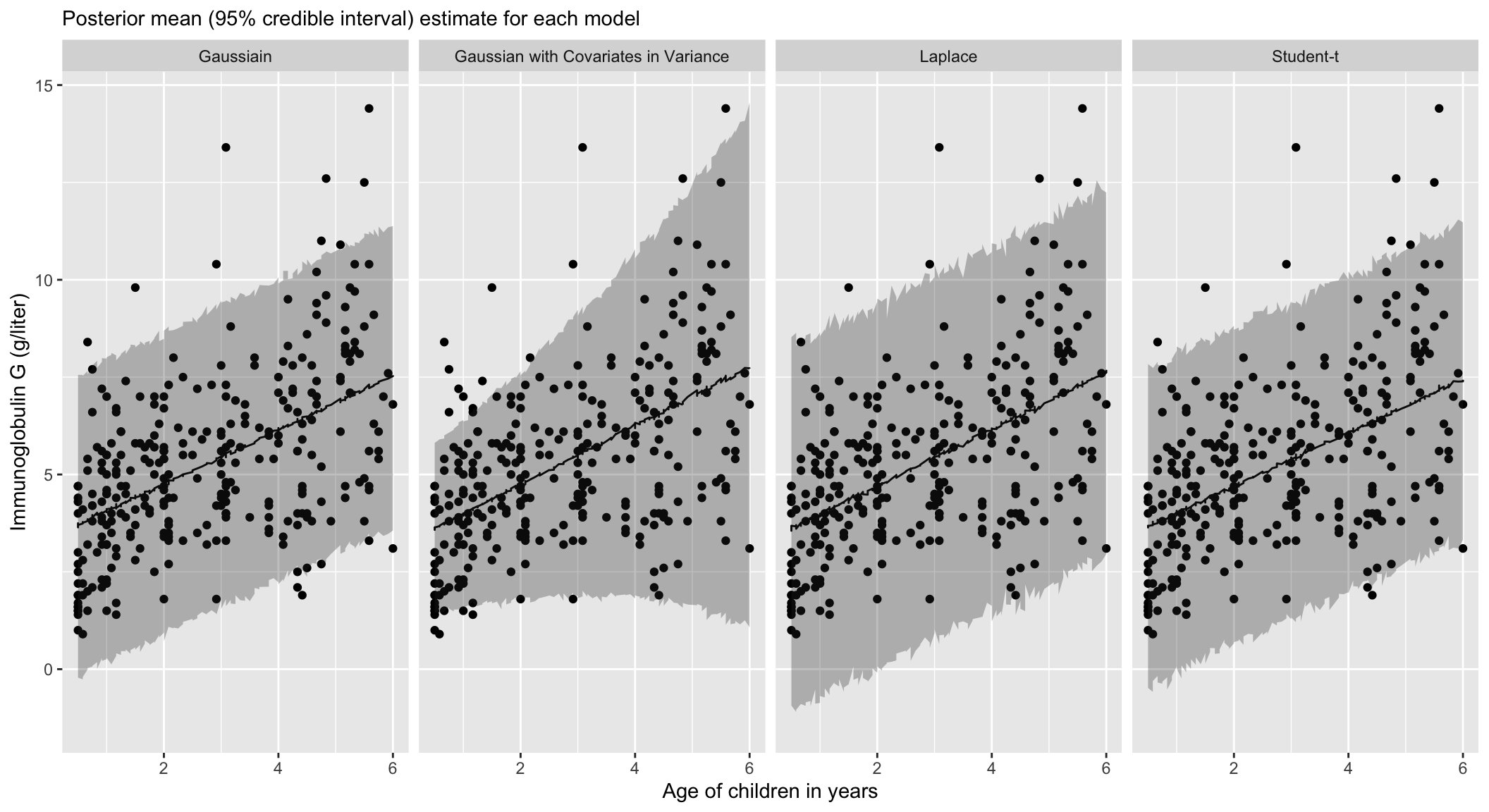
Posterior of
| Model | Mean | Lower | Upper |
|---|---|---|---|
| Laplace | 0.73 | 0.56 | 0.89 |
| Student-t | 0.69 | 0.55 | 0.82 |
| Gaussian | 0.69 | 0.56 | 0.83 |
| Gaussian with Covariates in Variance | 0.76 | 0.62 | 0.89 |
Model Comparison
| elpd_diff | elpd_loo | looic | |
|---|---|---|---|
| Student-t | 0.00 | -624.42 | 1248.84 |
| Gaussian | -2.01 | -626.43 | 1252.86 |
| Gaussian with Covariates in Variance | -6.09 | -630.51 | 1261.02 |
| Laplace | -13.10 | -637.52 | 1275.05 |
Examining the Student-t model fit
Inference for Stan model: anon_model.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 97.5% n_eff Rhat
alpha 3.32 0.00 0.21 2.91 3.74 2084 1
beta[1] 0.69 0.00 0.07 0.55 0.82 2122 1
sigma 1.72 0.00 0.10 1.53 1.91 2744 1
nu 7.80 0.05 2.35 4.40 13.29 2617 1
Samples were drawn using NUTS(diag_e) at Sun Feb 9 14:54:53 2025.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).Examining the Student-t model fit
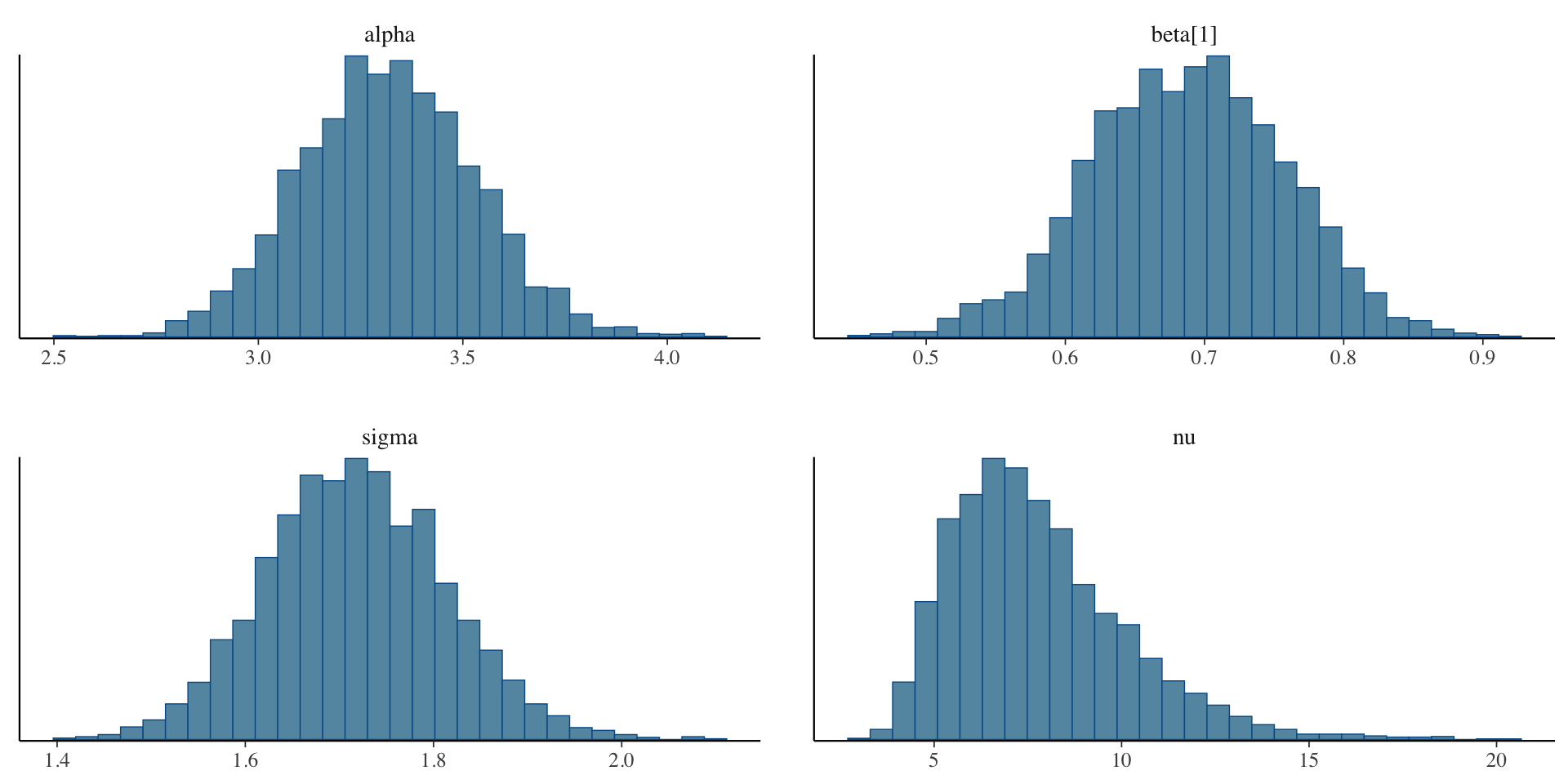
Examining the Student-t model fit
Summary of robust regression
Robust regression techniques can be used when the assumptions of constant variance and/or normality of the residuals do not hold.
Heteroskedastic variance can viewed as inducing extreme value distributions.
Extreme value regression using Student-t and Laplace distributions are robust to outliers.
Laplace regression is equivalent to median regression.
Prepare for next class
Work on HW 02, which is due before next class.
Complete reading to prepare for next Thursday’s lecture
Thursday’s lecture: Regularization